Question

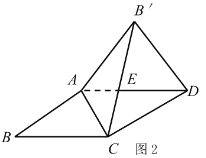
【题目】定义：两个相似等腰三角形，如果它们的底角有一个公共的顶点，那么把这两个三角形称为“关联等腰三角形”．如图，在与中， ，且所以称与为“关联等腰三角形”，设它们的顶角为，连接，则称会为“关联比"．

下面是小颖探究“关联比”与α之间的关系的思维过程，请阅读后，解答下列问题：

[特例感知]

当与为“关联等腰三角形”，且时，

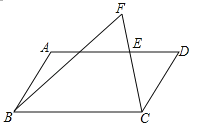
①在图1中，若点落在上，则“关联比”=

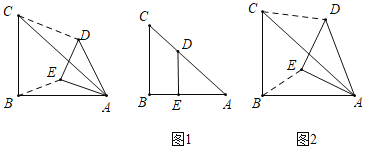
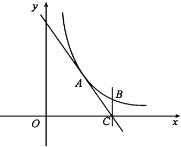
②在图2中，探究与的关系，并求出“关联比”的值．

[类比探究]

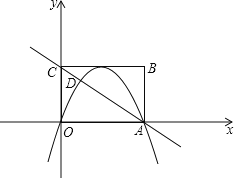
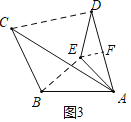
如图3，

①当与为“关联等腰三角形”，且时，“关联比”=

②猜想：当与为“关联等腰三角形”，且时，“关联比”= (直接写出结果，用含的式子表示)

[迁移运用]

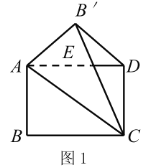
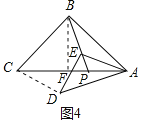
如图4， 与为“关联等腰三角形”．若点为边上一点，且，点为上一动点，求点自点运动至点时，点所经过的路径长．

Answer 1

【答案】（1）①；②；（2）①；②；（3）

【解析】

（1）①由α=90°可得△ABC与△AED为等腰直角三角形，斜边AC=AB，AD=AE，而DC=AC-AD，EB=AB-AE，代入计算即求得＝．

②由△ABC与△AED为等腰直角三角形可得∠BAC=∠EAD=45°，减去公共角∠CAE得∠CAD=∠BAE，再加上两夹边成比例，证得△CAD∽△BAE，所以等于相似比．

（2）①过点E作EF⊥AD于点F，由α=120°可得∠EAD=30°，所以得到Rt△AED的三边比，则AE=2EF，AF=EF，进而有AD=2AF=2EF，代入计算即求得＝．

②由α=n°可得∠EAD=90°-，又因为cos∠EAD=，所以得AF=AEcos（90°-），AD=2AF=2AEcos（90°-），根据①的证明过程可得＝=2cos（90°-）．

（3）过点B作BF⊥AC于点F，根据等腰直角三角形的条件求得PB的长，即求得点E自点B运动至点P时BE的长．连接CD，由（1）②的证明过程可知△CAD∽△BAE，所以∠ACD=∠ABE为一个定角，即点D所经过的路径是线段CD．根据“关联比”的值为，求得CD=EB=×＝．

解：（1）①∵当时,与为等腰直角三角形

故答案为：

②当时，

均为等腰直角三角形

又

“关联比”为

①过点E作EF⊥AD于点F
∴∠AFE=90°
∵AE=DE，∠AED=α=120°

∴∠EAD=∠EDA=30°，AF=DF

∴AE=2EF，AF=EF

∴AD=2AF=2EF

∴

同理可证：∠BAC=30°，

∴∠EAD+∠CAE=∠BAC+∠CAE
即∠CAD=∠BAE
∴△CAD∽△BAE

故答案为：．

②过点E作EF⊥AD于点F

中，

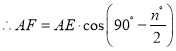
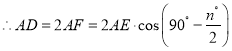
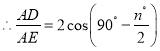
由①的证明过程可得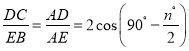

故答案为：2cos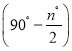

如图，过点作于点

∵与为“关联等腰三角形"，

，

与均为等腰直角三角形，

∵

连接，由上可知．≌

=定角，

点所经过的路径是线段

∵时，“关联比”为，

当点自点运动至点时，

点所经过的路径