Question

【题目】在平面直角坐标系中，点A的坐标是（0，3），点B的坐标是（－4，0）.

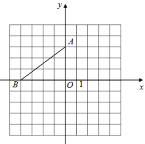
（1）画出△AOB绕点A逆时针旋转90°后得到的图形△A1O1B1；并写出点B1的坐标 ；

（2）画出△AOB关于点P（0，－1）的中心对称图形△A2O2B2，并写出点B2的坐标 ；

（3）若点Q为x轴上的一点，当B1Q+B2 Q的和最小时，直接写出点Q的坐标.

Answer 1

【答案】（1）见解析，点B1的坐标为（3，-1）；（2）见解析，点B2的坐标为：（4，-2）；（3）Q（，0）．

【解析】

（1）根据△AOB绕点A逆时针旋转90°得到的△A1O1B1，即可得到点B1的坐标；

（2）依据△AOB关于点P（0，－1）成中心对称的三角形为△A2O2B2，即可写出点B2的坐标．

（3）作点B1关于x轴的对称点B1′，连接B1′B2交x轴于点Q，则点Q即为所求点，利用待定系数法求出直线B1′B2的解析式，令x=0，求出y的值即可得出P点坐标．

（1）如图所示，点B1的坐标为（3，-1）；

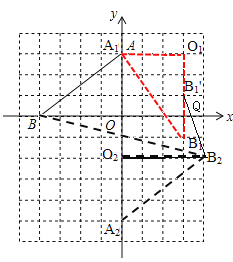
（2）如图所示，点B2的坐标为：（4，-2）；

（3）（2）设直线B1′B2的解析式为y=kx+b（k≠0），

∵B1的坐标为（3，-1），

∴B1′的坐标为（3，1），

∵B2的坐标为（4，-2），

∴，解得

∴直线B1′B2的解析式为y=-3x+10，

∵当y=0时，x=，

∴Q（，0）．