题目内容
等腰三角形的三边长分别为：x+3、2x+1、11，则x= ．
8或5
试题分析：题目中没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形.
当
时，解得
，三边长分别为5、5、11，而
，此时无法构成三角形；当
时，解得
，三边长分别为11、17、11，此时可以构成三角形当
时，解得
，三边长分别为8、11、11，此时可以构成三角形所以
或5.点评：已知没有明确腰和底边的题目一定要想到分类讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
相关题目
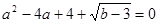，则笫三边c的长度是_____.