题目内容
【题目】(问题)
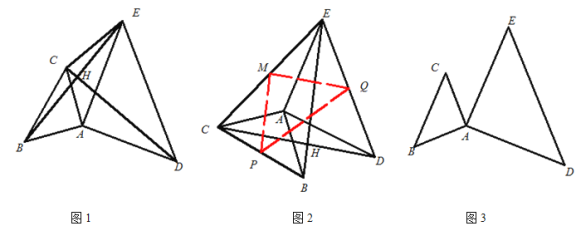
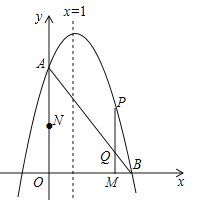
如图1,在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() .
.![]() ,点
,点![]() 在直线
在直线![]() 上移动,角的一边
上移动,角的一边![]() 始终经过点
始终经过点![]() ,另一边
,另一边![]() 与
与![]() 交于点
交于点![]() ,研究
,研究![]() 和
和![]() 的数量关系.
的数量关系.
(探究发现)
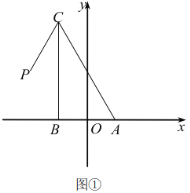
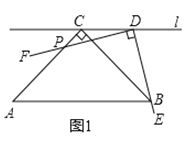
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点![]() 移动到使点
移动到使点![]() 与点
与点![]() 重合时,通过推理就可以得到
重合时,通过推理就可以得到![]() ,请写出证明过程;
,请写出证明过程;
(数学思考)
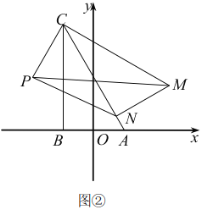
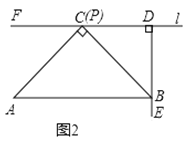
(2)如图3,若点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ),受(1)的启发,这个小组过点
),受(1)的启发,这个小组过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,就可以证明
,就可以证明![]() ,请完成证明过程;
,请完成证明过程;
(拓展引申)
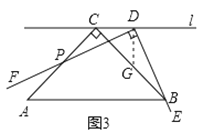
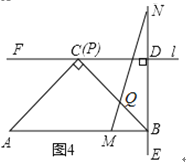
(3)如图4,在(1)的条件下,![]() 是
是![]() 边上任意一点(不含端点
边上任意一点(不含端点![]() ),
),![]() 是射线
是射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,这个数学兴趣小组经过多次取
,这个数学兴趣小组经过多次取![]() 点反复进行实验,发现点
点反复进行实验,发现点![]() 在某一位置时
在某一位置时![]() 的值最大.若
的值最大.若![]() ,请你直接写出
,请你直接写出![]() 的最大值.
的最大值.
【答案】【探究发现】(1)见解析;【数学思考】(2)见解析;【拓展引申】(3)![]() 时,
时,![]() 有最大值为2.
有最大值为2.
【解析】
根据等腰三角形的性质及平行的定义即可解得
根据证明![]() 即可推出
即可推出![]()
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可证明
,可证明![]() ,再推出
,再推出![]() 即可得
即可得![]() =
=![]() ,则
,则![]() .
.
证明:【探究发现】
(1)∵![]()
∴![]()
∵![]()
∴![]() ,且
,且![]()
∴![]()
∴![]()
即![]()
【数学思考】
(2)∵![]()
∴![]()
∴![]() ,
,
∵![]()
∴![]() ,且
,且![]() ,
,
∴![]()
∴![]()
【拓展引申】
(3)如图4,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
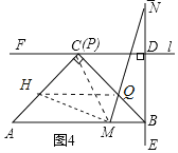
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() ,且
,且![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点共圆,
四点共圆,
∴![]()
∴![]() ,且
,且![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 时,
时,![]() 有最大值为2.
有最大值为2.

【题目】在“新冠肺炎防控”知识宣传活动中,某社区对居民掌握新冠肺炎防控知识的情况进行调查.其中![]() 、
、![]() 两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
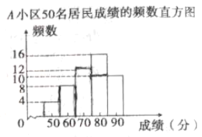
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,![]() 小区从左往右第四组的成绩如下
小区从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 、
、![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 |
| 277 | |
| 75.1 | 77 | 76 |
| 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区500名居民中能超过平均数的有多少人?
小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析![]() ,
,![]() 两小区居民掌握新冠防控知识的情况.
两小区居民掌握新冠防控知识的情况.