题目内容
【题目】在平面直角坐标系中,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 在第二象限,点
在第二象限,点![]() .
.
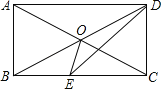
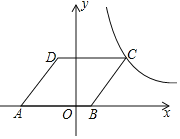
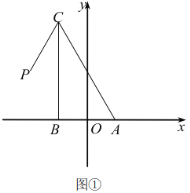
(1)如图①,求![]() 点坐标及
点坐标及![]() 的大小;
的大小;
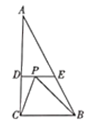
(2)将![]() 绕
绕![]() 点逆时针旋转得到
点逆时针旋转得到![]() ,点
,点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() ,
,![]() 为
为![]() 的面积.
的面积.
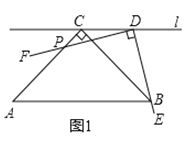
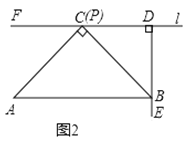
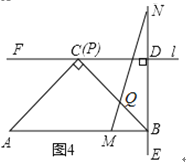
①如图②,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值;
的值;
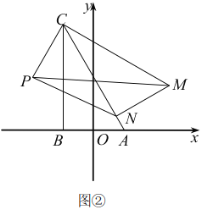
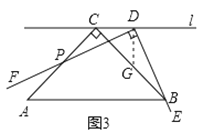
②求![]() 的取值范围(直接写出结果即可)
的取值范围(直接写出结果即可)
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)根据已知点点![]() ,点
,点![]() ,
,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() ,利用三角函数即可求出点C坐标;再过点
,利用三角函数即可求出点C坐标;再过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,构建直角三角形利用三角函数求角度;
,构建直角三角形利用三角函数求角度;
(2)①本题所求的是三角形面积,MN长度已知,做辅助线把三角形的高转移到AC上,利用![]() ,解直角三角形求出GN即可;
,解直角三角形求出GN即可;
②在△CNP中,GN是所求三角形的高,当GN=CN-CP时,三角形面积最小,当GN=CN+CP时,三角形面积最大.
(1)∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
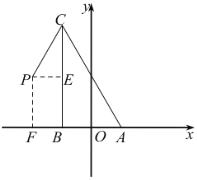
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,
可证得四边形![]() 是矩形.
是矩形.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
在![]() 中,∵
中,∵![]() ,
,
∴![]() .
.
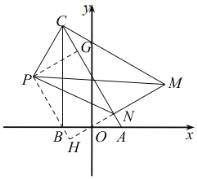
(2)①过点![]() 作
作![]() 直线
直线![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
可证得四边形![]() 是矩形.
是矩形.
∴![]() .
.
∵![]() 是由
是由![]() 旋转得到,
旋转得到,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
由(1)得![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
②![]() .
.
当P,C,N共线,PN=PC+CN时,S最大;
![]() ;
;
当P,C,N共线,PN=PC-CN时,S最小;
![]() ;
;
即![]() .
.

练习册系列答案
相关题目