Question

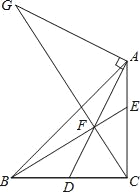
【题目】如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，连结OA、OB、OC，延长BO与AC交于点D，与⊙O交于点F，延长BA到点G，使得∠BGF＝∠GBC，连接FG．

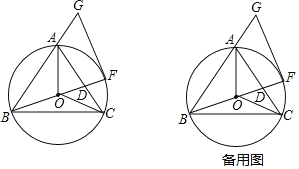
（1）求证：FG是⊙O的切线；

（2）若⊙O的半径为6．

①当OD＝4，求AD的长度；

②当△OCD是直角三角形时，求△ABC的面积．

Answer 1

【答案】（1）见解析；（2）①AD＝，② 当∠ODC＝90°时，S△ABC＝ ，当∠COD＝90°时，S△ABC＝

【解析】

（1）连接AF，分别证∠BGF+∠AFG=90°，∠BGF=∠AFB，即可得∠OFG=90°，进一步得出结论；

（2）①连接CF，则∠ACF=∠ABF，证△ABO≌△ACO，推出∠CAO=∠ACF，证△ADO∽△CDF，可求出DF，BD的长，再证△ADB∽△FDC，可推出ADCD＝20，即，可写出AD的长；

②因为△ODC为直角三角形，∠DCO不可能等于90°，所以存在∠ODC=90°或∠COD=90°，分两种情况讨论：当∠ODC=90°时，求出AD，AC的长，可进一步求出△ABC的面积；当∠COD=90°时，△OBC是等腰直角三角形，延长AO交BC于点M，可求出MO，AM的长，进一步可求出△ABC的面积．

（1）连接AF，

∵BF为⊙O的直径，

∴∠BAF=90°，∠FAG=90°，

∴∠BGF+∠AFG=90°，

∵AB=AC，

∴∠ABC=∠ACB，

∵∠ACB=∠AFB，∠BGF=∠ABC，

∴∠BGF=∠AFB，

∴∠AFB+∠AFG=90°，即∠OFG=90°，

又∵OF为半径，

∴FG是⊙O的切线；

（2）①连接CF，

则∠ACF=∠ABF，

∵AB=AC，AO=AO，BO=CO，

∴△ABO≌△ACO（SSS），

∴∠ABO=∠BAO=∠CAO=∠ACO，

∴∠CAO=∠ACF，

∴AO∥CF，

∴，

∵半径是6，OD=4，

∴DF=2，BD=10，

∴，即，

∵∠ABD=∠FCD，∠ADB=∠FDC，

∴△ADB∽△FDC，

∴，

∴ADCD=BDDF，

∴ADCD=20，即，

∴AD＝（取正值）；

②∵△ODC为直角三角形，∠DCO不可能等于90°，

∴存在∠ODC=90°或∠COD=90°，

当∠ODC=90°时，

∵∠ACO=∠ACF，

∴OD=DF=3，BD=9，

∴AD=CD，

∴ADCD=AD2=27，

∴，，

∴；

当∠COD=90°时，

∵OB=OC=6，

∴△OBC是等腰直角三角形，

∴，

延长AO交BC于点M，

则AM⊥BC，

∴，

∴，

∴，

∴△ABC的面积为：当∠ODC＝90°时，S△ABC＝ ，当∠COD＝90°时，S△ABC＝.