题目内容
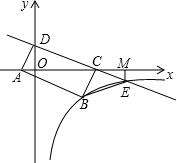 如图,直线y=-
如图,直线y=-| 1 |
| 2 |
| k |
| x |
分析:欲求S四BEMC,可将化为求S△BEC和S△EMC,根据题意,两三角形均为直角三角形,故只需求出B到CD的距离和E、C两点的坐标即可.
解答:解:根据题意,直线y=-
x+2与x轴交于C,与y轴交于D,
分别令x=0,y=0,
得y=2,x=4,
即D(0,2),C(4,0),
即DC=2
,
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+2,
令y=0,得x=-1,
即A(-1,0),
同理可得B点的坐标为B(3,-2)
又B为双曲线y=
(k<0)上,
代入得k=-6.
即双曲线的解析式为y=
与直线DC联立,
,
得
和
根据题意,
不合题意,
故点E的坐标为(6,-1).
所以BC=
,CE=
,
CM=2,EM=1,
所以S△BEC=
×BC×EC=
,
S△EMC=
×EM×CM=1,
故S四BEMC=S△BEC+S△EMC=
.
故答案为:
.
| 1 |
| 2 |
分别令x=0,y=0,
得y=2,x=4,
即D(0,2),C(4,0),
即DC=2
| 5 |
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+2,
令y=0,得x=-1,
即A(-1,0),
同理可得B点的坐标为B(3,-2)
又B为双曲线y=
| k |
| x |
代入得k=-6.
即双曲线的解析式为y=
| -6 |
| x |
与直线DC联立,

|
得
|
|
根据题意,
|
故点E的坐标为(6,-1).
所以BC=
| 5 |
| 5 |
CM=2,EM=1,
所以S△BEC=
| 1 |
| 2 |
| 5 |
| 2 |
S△EMC=
| 1 |
| 2 |
故S四BEMC=S△BEC+S△EMC=
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题综合考查了直线方程和双曲线方程的解答,以及对四边形面积的求解.

练习册系列答案
相关题目
 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( ) 点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止. 如图,直线
如图,直线 如图,直线
如图,直线