题目内容
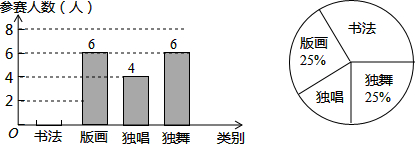
学校以班为单位举行了“书法、版画、独唱、独舞”四项预选赛,参赛总人数达480人之多,下面是七年级一班此次参赛人数的两幅不完整的统计图,请结合图中信息解答下列问题:
(1)求该校七年一班此次预选赛的总人数;
(2)补全条形统计图,并求出书法所在扇形圆心角的度数;
(3)若此次预选赛一班共有2人获奖,请估算本次比赛全学年约有多少名学生获奖?
(1)求该校七年一班此次预选赛的总人数;
(2)补全条形统计图,并求出书法所在扇形圆心角的度数;
(3)若此次预选赛一班共有2人获奖,请估算本次比赛全学年约有多少名学生获奖?

考点:条形统计图,用样本估计总体,扇形统计图
专题:
分析:(1)用七年一班版画人数除以版画的百分数即可求得七年一班的参赛人数;
(2)用七年一班总的参赛人数减去版画、独唱、独舞的参赛人数即可求得书法的参赛人数,再用七年一班书法的参赛人数除以七年一班总的参赛人数再乘以360°即可求得七年一班书法所在扇形圆心角的度数,根据求得的数据补全统计图即可;
(3)用参赛总人数除以七年一班的参赛人数,再乘以2即可求解.
(2)用七年一班总的参赛人数减去版画、独唱、独舞的参赛人数即可求得书法的参赛人数,再用七年一班书法的参赛人数除以七年一班总的参赛人数再乘以360°即可求得七年一班书法所在扇形圆心角的度数,根据求得的数据补全统计图即可;
(3)用参赛总人数除以七年一班的参赛人数,再乘以2即可求解.
解答:解:(1)6÷25%=24(人).
故该校七年一班此次预选赛的总人数是24人;
(2)24-6-4-6=8(人),
书法所在扇形圆心角的度数8÷24×360°=120°;
补全条形统计图如下:

(3)480÷24×2
=20×2
=40(名).
故本次比赛全学年约有40名学生获奖.
故该校七年一班此次预选赛的总人数是24人;
(2)24-6-4-6=8(人),
书法所在扇形圆心角的度数8÷24×360°=120°;
补全条形统计图如下:

(3)480÷24×2
=20×2
=40(名).
故本次比赛全学年约有40名学生获奖.
点评:本题考查了条形统计图与扇形统计图的知识,解题的关键是从两种统计图中整理出进一步解题的有关信息.

练习册系列答案
相关题目
矩形不一定具有的特征是( )
| A、对角线相等 |
| B、四个角是直角 |
| C、对边分别相等 |
| D、对角线互相垂直 |
如果二次函数y=(x-h)2+k(hk≠0)的图象经过原点,那么分式
的值是( )
| h2 |
| k |
| A、0 | B、1 | C、-1 | D、0或1 |
已知正△AOB的三个顶点都在抛物线y=
x2上,其中O为坐标原点,则正△AOB的面积为( )
| 1 |
| 2 |
A、4
| ||
B、12
| ||
C、6
| ||
| D、24 |
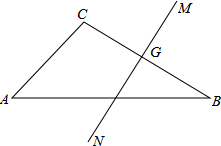 如图,△ABC中,NM是BC边的垂直平分线,垂足为G.
如图,△ABC中,NM是BC边的垂直平分线,垂足为G.
 如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E. 抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.
抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.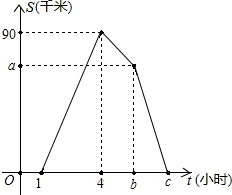 甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.
甲、乙两人同时从家乘车去书店,途中甲因故下车,改骑自行车前往书店(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达书店停留2小时后,以另一速度返回,2小时后与甲相遇.下图为甲、乙两人之间的距离S(千米)与行驶时间t(小时)之间的函数关系.