题目内容
19.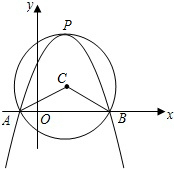 如图,在平面直角坐标系中,设点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且顶点P在⊙C上.
如图,在平面直角坐标系中,设点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且顶点P在⊙C上.(1)写出A,B两点的坐标;
(2)试确定此抛物线的解析式
(3)在该抛物线是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)过点C作DC⊥AB,垂足为D.由垂径定理可知:AD=DB,然后由勾股定理可求得AD的长,从而得到点A和点B的坐标;
(2)由图形的对称性可知P在CD上,从而可求得点P的坐标,设抛物线的解析式为y=a(x-1)2+3,将点B的坐标代入可得到a的值,从而可得到抛物线的解析式;
(3)取OP的中点E,连接CE,并延长CE到D使ED=CE.首先由线段的中点坐标公式求得点D的坐标,然后判断点D是否在抛物线上即可.
解答 解:如图1所示:过点C作DC⊥AB,垂足为D.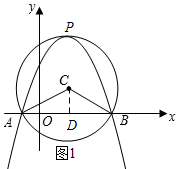
∵CD⊥AB,
∴AD=DB.
∵在Rt△ADC中,AC=2,CD=1,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{3}$.
∴DB=$\sqrt{3}$.
∴A(1-$\sqrt{3}$,0)、B(1$+\sqrt{3}$,0).
(2)如图1所示:
∵点A与点B关于CD对称,
∴CD为抛物线的对称.
∴点P在CD上.
∵CD=1,CP=2,
∴PD=3.
∴P(1,3).
设抛物线的解析式为y=a(x-1)2+3.
∵将点B的坐标代入得:3a+3=0,解得:a=-1,
∴抛物线的解析式y=-(x-1)2+3,即y=-x2+2x+2.
(3)存在.
理由:如图2所示:取OP的中点E,连接CE,并延长CE到D使ED=CE.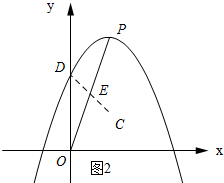
设点D的坐标为(x,y).
∵OP与CD相互平分,
∴$\frac{x+1}{2}=\frac{0+1}{2}$,$\frac{y+1}{2}=\frac{3+0}{2}$.
∴x=0,y=2.
∵将x=0代入抛物线的解析式得y=2,
∴点D在抛物线上.
∴当点D的坐标为(0,2)时,OP与CD相互平分.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了垂径定理、勾股定理、待定系数法求二次函数的解析式、线段的中点坐标公式,求得点P的坐标是解答问题(2)的关键;利用线段中点坐标公式求得点D的坐标是解答问题(3)的关键.

| A. |  | B. |  | C. |  | D. |  |
| A. | 2(x+y)2 | B. | 2(x-y)2 | C. | 2(x+y)(x-y) | D. | 2(y+x)(y-x) |
| A. |  | B. |  | C. |  | D. |  |

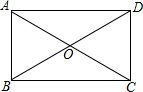 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.