题目内容
 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=
如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=6cm,DC=2cm,则AE=2
2
cm.分析:首先根据全等三角形的判定得出BDE≌△ADC,进而得出DE=CD,即可得出答案.
解答:解:∵BF⊥AC,
∴∠C+∠FBC=90°,
∵AD⊥BC,
∴∠C+∠DAC=90°,
∴∠DAC=∠FBC,
在△BDE和△ADC中
,
∴△BDE≌△ADC(ASA),
∴CD=DE=2cm,
∵BC=6cm,DC=2cm,
∴BD=AD=4cm,
∴AE=4-2=2(cm).
故答案为:2.
∴∠C+∠FBC=90°,
∵AD⊥BC,
∴∠C+∠DAC=90°,
∴∠DAC=∠FBC,
在△BDE和△ADC中
|
∴△BDE≌△ADC(ASA),
∴CD=DE=2cm,
∵BC=6cm,DC=2cm,
∴BD=AD=4cm,
∴AE=4-2=2(cm).
故答案为:2.
点评:此题主要考查了全等三角形的判定与性质,根据题意得出∠DAC=∠FBC是解题关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
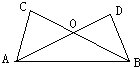 20、如图:AD⊥BD于D,BC⊥AC于C,,AC=BD,AD与BC相交于点O,
20、如图:AD⊥BD于D,BC⊥AC于C,,AC=BD,AD与BC相交于点O,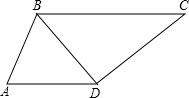 已知:如图,AD=BD=CD=m,AB=n,BC=p,BC∥AD,m、n为有理数.
已知:如图,AD=BD=CD=m,AB=n,BC=p,BC∥AD,m、n为有理数. 如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70度.求∠AED的度数.
如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70度.求∠AED的度数. 如图,AD⊥BD,垂足为D,AE平分∠BAC,∠B=30°,∠DAC=20度.求∠AED的度数.
如图,AD⊥BD,垂足为D,AE平分∠BAC,∠B=30°,∠DAC=20度.求∠AED的度数.