题目内容
 如图,AD⊥BD,垂足为D,AE平分∠BAC,∠B=30°,∠DAC=20度.求∠AED的度数.
如图,AD⊥BD,垂足为D,AE平分∠BAC,∠B=30°,∠DAC=20度.求∠AED的度数.
分析:首先根据直角三角形的两个锐角互余求得∠ACD的值.再根据三角形的外角性质和角平分线的概念求得∠BAE的度数,最后根据三角形的一个外角等于和它不相邻的两个内角和求得∠AED的度数.
解答:解:∵AD⊥BD,∠DAC=20°,
∴∠ACD=90°-∠DAC=70°.
又∵∠ACD=∠CAB+∠B,
∴∠CAB=∠ACD-∠B=40°,
∴∠EAB=
∠CAB=20°,
∴∠AED=∠EAB+∠B=50°.
∴∠ACD=90°-∠DAC=70°.
又∵∠ACD=∠CAB+∠B,
∴∠CAB=∠ACD-∠B=40°,
∴∠EAB=
| 1 |
| 2 |
∴∠AED=∠EAB+∠B=50°.
点评:运用的知识点有直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角和;角平分线的概念.

练习册系列答案
相关题目
 4、如图,下列说法不正确的是( )
4、如图,下列说法不正确的是( )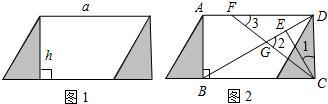 23、如图1,过平行四边形纸片的一个顶点作它的一条垂线段h,沿这条垂线段剪下三角形纸片,将它平移到右边,平移距离等于平行四边形的底边长a.
23、如图1,过平行四边形纸片的一个顶点作它的一条垂线段h,沿这条垂线段剪下三角形纸片,将它平移到右边,平移距离等于平行四边形的底边长a.


 2、如图所示,下列说法正确的是( )
2、如图所示,下列说法正确的是( ) 如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是( )
如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是( )