题目内容
在Rt△ABC中,AC=5,AB=12,∠A=90°,以A为圆心,r为半径作⊙O与斜边BC有唯一公共点,则r的取值范围是 .
考点:直线与圆的位置关系
专题:计算题
分析:先利用勾股定理计算出BC=13,再利用面积法计算出AD=
,然后分类讨论:当r=AD=
时,BC与⊙A相切于D,⊙A与斜边BC有唯一公共点;当5<r≤12时,斜边BC与⊙A相交,且只有一个公共点.
| 60 |
| 13 |
| 60 |
| 13 |
解答:解:作AD⊥BC于D,如图,
在Rt△ABC中,∵AC=5,AB=12,
∴BC=
=13,
∵
AC•AB=
AD•BC,
∴AD=
,
当r=AD=
时,BC与⊙A相切于D,⊙A与斜边BC有唯一公共点;
当5<r≤12时,⊙A与斜边BC有唯一公共点.
故答案为r=
或5<r≤12.

在Rt△ABC中,∵AC=5,AB=12,
∴BC=
| AB2+AC2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| 60 |
| 13 |
当r=AD=
| 60 |
| 13 |
当5<r≤12时,⊙A与斜边BC有唯一公共点.
故答案为r=
| 60 |
| 13 |
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,当直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
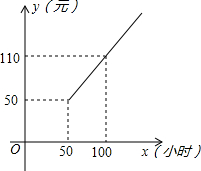 某小区宽带收费的方式有甲、乙两种:
某小区宽带收费的方式有甲、乙两种: