题目内容
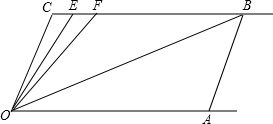 已知如图,射线CB∥OA,∠C=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
已知如图,射线CB∥OA,∠C=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠EOB的度数;
(2)写出∠OBC与∠OFC的数量关系,并说明理由;
(3)若AB∥OC,∠OEC=∠OBA,求出∠OEC的度数.
考点:平行线的性质
专题:
分析:(1)根据两直线平行,同旁内角互补求出∠AOC,再根据角平分线的定义求出∠EOB=
∠AOC;
(2)根据两直线平行,内错角相等可得∠OBC=∠AOB,从而得到∠AOF=2∠OBC,再根据两直线平行,内错角相等可得∠OFC=∠AOF,从而得解;
(3)根据两直线平行,内错角相等可得∠OEC=∠AOE,∠OBA=∠BOC,然后求出∠COE=∠AOB,从而确定出OE、OF、OB是∠AOC的四等分线,然后求出∠AOE,从而得解.
| 1 |
| 2 |
(2)根据两直线平行,内错角相等可得∠OBC=∠AOB,从而得到∠AOF=2∠OBC,再根据两直线平行,内错角相等可得∠OFC=∠AOF,从而得解;
(3)根据两直线平行,内错角相等可得∠OEC=∠AOE,∠OBA=∠BOC,然后求出∠COE=∠AOB,从而确定出OE、OF、OB是∠AOC的四等分线,然后求出∠AOE,从而得解.
解答:解:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
又∵∠FOB=∠AOB,
∴∠EOB=
∠AOC=
×80°=40°;
(2)∵CB∥OA,
∴∠OBC=∠AOB,
∴∠AOF=∠FOB+∠AOB=2∠OBC,
∵CB∥OA,
∴∠OFC=∠AOF=2∠OBC;
(3)∵CB∥OA,
∴∠OEC=∠AOE,
∵AB∥OC,
∴∠OBA=∠BOC,
∵∠OEC=∠OBA,
∴∠AOE=∠BOC,
∴∠AOE-∠BOE=∠BOC-∠BOE,
即∠COE=∠AOB,
∴OE、OF、OB是∠AOC的四等分线,
∴∠AOE=
×80°=60°,
∵CB∥OA,
∴∠OEC=∠AOE=60°.
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COF,
∴∠COE=∠EOF,
又∵∠FOB=∠AOB,
∴∠EOB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵CB∥OA,
∴∠OBC=∠AOB,
∴∠AOF=∠FOB+∠AOB=2∠OBC,
∵CB∥OA,
∴∠OFC=∠AOF=2∠OBC;
(3)∵CB∥OA,
∴∠OEC=∠AOE,
∵AB∥OC,
∴∠OBA=∠BOC,
∵∠OEC=∠OBA,
∴∠AOE=∠BOC,
∴∠AOE-∠BOE=∠BOC-∠BOE,
即∠COE=∠AOB,
∴OE、OF、OB是∠AOC的四等分线,
∴∠AOE=
| 3 |
| 4 |
∵CB∥OA,
∴∠OEC=∠AOE=60°.
点评:本题考查了平行线的性质,角平分线的定义,熟记性质与概念并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC=10cm,BD=8cm,边AB=6cm,则△DOC的周长为
如图,在平行四边形ABCD中,对角线AC、BD交于点O,AC=10cm,BD=8cm,边AB=6cm,则△DOC的周长为