题目内容
多边形的边数增加4,则内角和增加 度,而外角和= 度.
考点:多边形内角与外角
专题:
分析:利用n边形的内角和公式(n-2)•180°(n≥3)且n为整数),多边形外角和为360°即可解决问题.
解答:解:根据n边形的内角和可以表示成(n-2)•180°,
可以得到增加一条边时,边数变为n+4,
则内角和是(n+3)•180°,因而内角和增加:(n+3)•180°-(n-2)•180°=4×180°=720°.
多边形外角和为360°,
故答案为:720;360°.
可以得到增加一条边时,边数变为n+4,
则内角和是(n+3)•180°,因而内角和增加:(n+3)•180°-(n-2)•180°=4×180°=720°.
多边形外角和为360°,
故答案为:720;360°.
点评:本题主要考查了多边形的内角和公式和外角和,是需要熟练掌握的内容.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于D,∠C=80°,则∠D的度数是( )
如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于D,∠C=80°,则∠D的度数是( )| A、40° | B、45° |
| C、50° | D、55° |
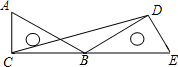 把两块含30°角的相同的直角三角板按如图所示摆放,使点C、B、E在同一直线上,连接CD,则∠CDB的度数为( )
把两块含30°角的相同的直角三角板按如图所示摆放,使点C、B、E在同一直线上,连接CD,则∠CDB的度数为( )| A、15° | B、18° |
| C、25° | D、30° |
 如图,BC∥DE,AD⊥DF,∠l=30°,∠2=50°,则∠A=
如图,BC∥DE,AD⊥DF,∠l=30°,∠2=50°,则∠A=