题目内容
已知:如图,在平面直角坐标系 中,抛物线
中,抛物线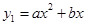 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ).
).

(1)求抛物线 的解析式;
的解析式;
(2)将抛物线 沿x轴翻折得抛物线
沿x轴翻折得抛物线 ,求抛物线
,求抛物线 的解析式;
的解析式;
(3)在(2)的条件下,抛物线 上是否存在点M,使
上是否存在点M,使 与
与 相似?如果存在,求出点M的坐标;如果不存在,说明理由.
相似?如果存在,求出点M的坐标;如果不存在,说明理由.
 中,抛物线
中,抛物线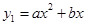 过点A(6,0)和点B(3,
过点A(6,0)和点B(3, ).
).
(1)求抛物线
 的解析式;
的解析式;(2)将抛物线
 沿x轴翻折得抛物线
沿x轴翻折得抛物线 ,求抛物线
,求抛物线 的解析式;
的解析式;(3)在(2)的条件下,抛物线
 上是否存在点M,使
上是否存在点M,使 与
与 相似?如果存在,求出点M的坐标;如果不存在,说明理由.
相似?如果存在,求出点M的坐标;如果不存在,说明理由.(1)  ;(2)
;(2)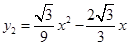 ;(3)
;(3)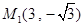 ,
,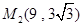 ,
, .
.
 ;(2)
;(2)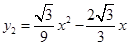 ;(3)
;(3)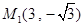 ,
,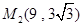 ,
, .
.试题分析:(1)把A、B两点坐标代入y1=ax2+bx,求得a、b的值,从而确定y1的解析式;
(2)将抛物线
 沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点
沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点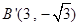 .从而可求y2的解析式;
.从而可求y2的解析式;(3)过点B作BC⊥x轴于点C,易证
 是顶角为120º的等腰三角形.分两种情况讨论:①当点M在x轴下方时,
是顶角为120º的等腰三角形.分两种情况讨论:①当点M在x轴下方时, 就是
就是 ,此时点M的坐标为
,此时点M的坐标为 .②当点M在x轴上方时,此时点M的坐标为(9,
.②当点M在x轴上方时,此时点M的坐标为(9, )、
)、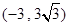 .
.试题解析:(1)依题意,得
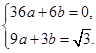 解得
解得
∴抛物线
 的解析式为
的解析式为
(2)将抛物线
 沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点
沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点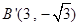 .
.设抛物线
 的解析式为
的解析式为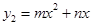 ,
,∴
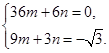 解得
解得
∴抛物线
 的解析式为
的解析式为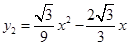 .
.(3)过点B作BC⊥x轴于点C,

则有
 .
.∴
 ,
,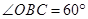 .
.∵OC=3,OA=6,
∴AC=3.
∴
 ,
, .
.∴OB=AB.
即
 是顶角为120º的等腰三角形.
是顶角为120º的等腰三角形.分两种情况:
①当点M在x轴下方时,
 就是
就是 ,此时点M的坐标为
,此时点M的坐标为 .
.②当点M在x轴上方时,假设

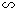
 ,则有AM=OA=6,
,则有AM=OA=6, .
.过点M作MD⊥x轴于点D,则
 .
.∴
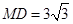 ,
,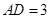 . ∴OD=9.
. ∴OD=9.而(9,
 )满足关系式
)满足关系式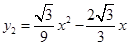 ,
,即点M在抛物线
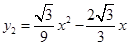 上.
上.根据对称性可知,点
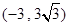 也满足条件.
也满足条件.综上所述,点M的坐标为
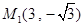 ,
,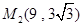 ,
, .
.考点:二次函数综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
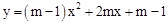 .
. 的图象与一次函数
的图象与一次函数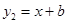 的图象交于
的图象交于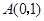 ,
, 两点. C
两点. C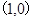 为二次函数图象的顶点.
为二次函数图象的顶点.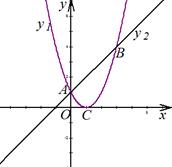
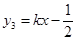 (k >0)与函数f的图象只有两个交点时,求
(k >0)与函数f的图象只有两个交点时,求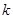 的值.
的值. 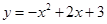 .
.
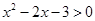 的解集.
的解集. ,
, 轴上有
轴上有 两点,以
两点,以 表示这两点间的距离,其中
表示这两点间的距离,其中 ,
, 的横坐标分别是方程组
的横坐标分别是方程组 的解,则
的解,则 的值等于 .
的值等于 . ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
 (x+1)2-1的顶点坐标为 .
(x+1)2-1的顶点坐标为 .  的图象完全重合的抛物线是( )
的图象完全重合的抛物线是( )


