Question

【题目】定义：在平面直角坐标系中，对于任意两点，，若点满足，，那么称点是点，的融合点.

例如：，，当点满是，时，则点是点，的融合点，

（1）已知点，，，请说明其中一个点是另外两个点的融合点.

（2）如图，点，点是直线上任意一点，点是点，的融合点.

①试确定与的关系式.

②若直线交轴于点，当为直角三角形时，求点的坐标.

Answer 1

【答案】（1）点是点，的融合点；（2）①，②符合题意的点为， .

【解析】

（1）由题中融合点的定义即可求得答案.

（2）①由题中融合点的定义可得，.

②结合题意分三种情况讨论：（ⅰ）时，画出图形，由融合点的定义求得点坐标；（ⅱ）时，画出图形，由融合点的定义求得点坐标；（ⅲ）时，由题意知此种情况不存在.

（1）解：，

∴点是点，的融合点

（2）解：①由融合点定义知，得．

又∵，得

∴，化简得．

②要使为直角三角形，可分三种情况讨论：

（i）当时，如图1所示，

设，则点为．

由点是点，的融合点，

可得或，

解得，∴点．

（ii）当时，如图2所示，

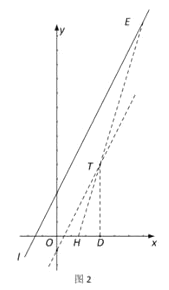
则点为．

由点是点，的融合点，

可得点．

（iii）当时，该情况不存在．

综上所述，符合题意的点为，