题目内容
观察算式,探究规律:
当n=1时,S1=13=1=12;
当n=2时,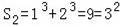
 ;
;
当n=3时,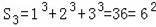
 ;
;
当n=4时,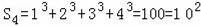
 ;
;
…
那么Sn与n的关系为( )
A.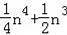
 B.
B.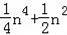
 C.
C.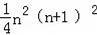
 D.
D.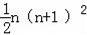

C【考点】规律型:数字的变化类.
【专题】规律型.
【分析】观察不难发现,底数是两个连续整数的乘积的一半,根据此规律写出即可.
【解答】解:∵3=
 ,6=
,6=
 ,10=
,10=
 ,
,
∴S1=(
 )2,
)2,
S2=(
 )2,
)2,
S3=(
 )2,
)2,
S4=(
 )2,
)2,
…
Sn=(
 )2=
)2=
 n2(n+1)2.
n2(n+1)2.
故选C.
【点评】本题是对数字变化规律的考查,难度较大,对同学们的数字敏感程度要求较高,观察出底数的变化特点是解题的关键.

练习册系列答案
相关题目



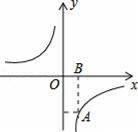




 在同一坐标系数中的大致图象是( )
在同一坐标系数中的大致图象是( )
 B.
B.
 C.
C.

