题目内容
 如图,圆M与y轴相切于点C,与x轴交于A(2-
如图,圆M与y轴相切于点C,与x轴交于A(2-| 3 |
| 3 |
 |
| AB |
 |
| AD |
| 1 |
| 2 |
 |
| BD |
考点:圆的综合题
专题:
分析:作ME⊥x轴于E,连接MC,根据垂径定理,由ME⊥AB得AE=BE=,则OE=OA+AE=2,再根据切线的性质得到MC⊥y轴,所以四边形MEOC为矩形,于是得到MC=OE=2,再连结OM,MQ,K点为OM的中点,连结NK,CK,先根据勾股定理计算出OM=
,根据直角三角形斜边上的中线性质得CK=
,易得NK为△OQM的中位线,则NK=
QM=1,根据三角形三边的关系得到,当∠CKN=180°时,CN最大,此时CN=CK+NK=
+1.
| 5 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答: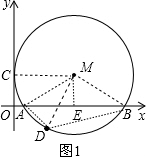 解:如图1,作ME⊥x轴于E,连接MC,
解:如图1,作ME⊥x轴于E,连接MC,
∵A(2-
,0)、点B(2+
,0),
∴AB=2
,
∵ME⊥AB,
∴AE=BE=
,
∴OE=OA+AE=2-
+
=2,
∵⊙M与y轴相切于点C,
∴MC⊥y轴,
∴四边形MEOC为矩形,
∴MC=OE=2,
即⊙M的半径为2,
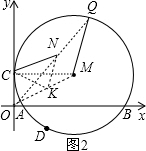 连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
∵OC=1,MC=2,
∴OM=
=
,
∴CK=
,
∵N点为OQ的中点,
∴NK为△OQM的中位线,
∴NK=
QM=1,
∵点Q是⊙M上一个动点,
∴当∠CKN=180°时,CN最大,此时CN=CK+NK=
+1,即CN的最大值为
+1.
 解:如图1,作ME⊥x轴于E,连接MC,
解:如图1,作ME⊥x轴于E,连接MC,∵A(2-
| 3 |
| 3 |
∴AB=2
| 3 |
∵ME⊥AB,
∴AE=BE=
| 3 |
∴OE=OA+AE=2-
| 3 |
| 3 |
∵⊙M与y轴相切于点C,
∴MC⊥y轴,
∴四边形MEOC为矩形,
∴MC=OE=2,
即⊙M的半径为2,
 连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,
连结OM,MQ,K点为OM的中点,连结NK,CK,如图2,∵OC=1,MC=2,
∴OM=
| 12+22 |
| 5 |
∴CK=
| ||
| 2 |
∵N点为OQ的中点,
∴NK为△OQM的中位线,
∴NK=
| 1 |
| 2 |
∵点Q是⊙M上一个动点,
∴当∠CKN=180°时,CN最大,此时CN=CK+NK=
| ||
| 2 |
| ||
| 2 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和切线的性质;会利用勾股定理计算线段的长;理解坐标与图形的性质;掌握三角形中位线定理和矩形的判定以及性质,题目的综合性较强,对学生的解题能力要求很高.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,在四边形ABCD中,AB∥CD,∠D=90°,以D为圆心,AD为半经的⊙D与直线BC相切于点E.求证:BC=CD.
如图,在四边形ABCD中,AB∥CD,∠D=90°,以D为圆心,AD为半经的⊙D与直线BC相切于点E.求证:BC=CD.