题目内容
3. 二次函数y=x2-2x-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点为D.
二次函数y=x2-2x-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点为D.(1)画出该二次函数的图象;
(2)求四边形OCDB的面积.
分析 (1)画出图形;
(2)分别求出C和D的坐标,利用梯形与三角形面积的和求四边形OCDB的面积.
解答 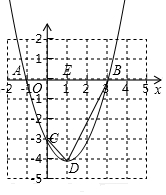 解:(1)如图所示,
解:(1)如图所示,
(2)y=x2-2x-3=(x-1)2-4,
∴C(0,-3),D(1,-4),
∴S四边形OCDB=S△DEB+S梯形OCDE,
=$\frac{1}{2}$DE•BE+$\frac{1}{2}$(OC+DE)×OE,
=$\frac{1}{2}$×4×2+$\frac{1}{2}$×(3+4)×1,
=4+3.5,
=7.5.
点评 本题考查了二次函数的图象与性质,根据解析式及对称性质会画函数的图象,求图形面积时,可以直接根据图形面积公式求解,也可以利用面积和或差求解.

练习册系列答案
相关题目
11.下列调查中,最适合采用普查方式的是( )
| A. | 调查一批灯泡的使用寿命 | |
| B. | 调查全国人民对延迟退休政策的态度 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国人民对里约奥运会的收视情况 |
8.把6960000000用科学记数法表示为( )
| A. | 696×108 | B. | 6.96×109 | C. | 6.96×1010 | D. | 0.696×1011 |
15.十一黄金周( 7 天)期间,萧红中学7年3班某同学计划租车去旅行,在看过租车公司的方案后,认为有以下两种方案比较适合(注:两种车型的油耗相同):
解决下列问题:
(1)如果此次旅行的总行程为800千米,请通过计算说明租用哪种型号的车划算;
(2)设本次旅行行程为x千米(x是正整数),请通过计算说明如何根据旅行行程选择省钱的租车方案.
| 周租金 (单位:元) | 免费行驶里程 (单位:千米) | 超出部分费用 (单位:元/千米) | |
| A型 | 1740 | 100 | 1.5 |
| B型 | 2640 | 220 | 1.2 |
(1)如果此次旅行的总行程为800千米,请通过计算说明租用哪种型号的车划算;
(2)设本次旅行行程为x千米(x是正整数),请通过计算说明如何根据旅行行程选择省钱的租车方案.