Question

11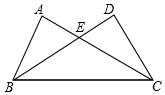．在△ABC和△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．
（1）求证：△ABC≌△DCB；
（2）当∠AEB=50°时，求∠EBC的度数．

Answer 1

分析 （1）先证明△ABE≌△DCE，得出AE=DE，BE=CE，证出AC=DB，再由SAS即可得出结论；
（2）只要证明∠ACB=∠DBC，由∠AEB=∠ECB+∠EBC=50°，即可解决问题．

解答 （1）证明：在Rt△ABE和Rt△DCE中，$\left\{\begin{array}{l}{∠A=∠D}&{\;}\\{∠AEB=∠DEC}&{\;}\\{AB=DC}&{\;}\end{array}\right.$，
∴△ABE≌△DCE（AAS），
∴AE=DE，BE=CE，
∴AC=DB，
在△ABC和△DCB中，$\left\{\begin{array}{l}{AB=DC}&{\;}\\{∠A=∠D}&{\;}\\{AC=DB}&{\;}\end{array}\right.$，
∴△ABC≌△DCB（SAS）；
（2）解：∵△ABC≌△DCB，
∴∠ACB=∠DBC，
∵∠AEB=∠ECB+∠EBC=50°，
∴∠EBC=25°．

点评 本题考查全等三角形的判定和性质，解题的关键是灵活应用全等三角形的判定和性质，属于中考常考题型．