题目内容
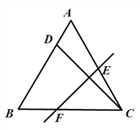
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,试说明四边形
,试说明四边形![]() 是菱形;
是菱形;
(3)在(2)的条件下,试确定![]() 点的位置,使得
点的位置,使得![]() ,并说明理由.
,并说明理由.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先根据SSS证明△ABC≌△ADC得∠BAC=∠DAC,则△ABF≌△ADF,再由对顶角相等可得结论;
(2)根据平行得内错角∠BAC=∠ACD,再由(1)的结论∠BAC=∠DAC,可证得AD=CD,则四边相等,四边形ABCD是菱形;
(3)当EB⊥CD时,∠EFD=∠BCD,理由是:证明△BCF≌△DCF,得∠CBF=∠CDF,则直角△EFD和直角△AEC有两个角对应相等,则∠EFD=∠BCD.
证明:(1)在![]() 和
和![]() 中,
中,
![]()
 ,
,
![]() ,
,
![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形;
是菱形;
(3)解:当![]() 时,
时,![]() ,
,
理由:![]() 四边形
四边形![]() 为菱形,
为菱形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
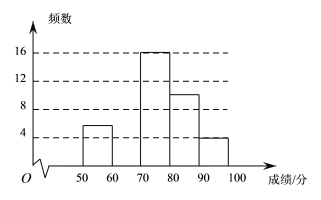
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 |
| 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | 4 | 0.08 |
(1)频数分布表中的![]() ;
;
(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
【题目】下表是某校七年级小朋友小敏这学期第一周和第二周做家务事的时间统计表,已知小敏每次在做家务事中洗碗的时间相同,扫地的时间也相同.
每周做家务总时间(分) | 洗碗次数 | 扫地的次数 | |
第一周 | 44 | 2 | 3 |
第二周 | 42 | 1 | 4 |
(1)求小敏每次洗碗的时间和扫地的时间各是多少?
(2)为鼓励小敏做家务,小敏的家长准备洗碗一次付12元,扫地一次付8元,总费用不超过100元。请问小敏如何安排洗碗与扫地的次数,既能够让花费的总时间最少,又能够全部拿到100元?