题目内容
(1)(-2)3×
+
×(
)2-
(2)
-3
+
(3)化简:|1-
|+|
-
|+|
-2|
(4)解方程 25(x-1)2-16=0.
| (-4)2 |
| 3 | (-4)3 |
| 1 |
| 2 |
| 81 |
(2)
| 32 |
|
| ||
|
(3)化简:|1-
| 2 |
| 2 |
| 3 |
| 3 |
(4)解方程 25(x-1)2-16=0.
分析:(1)原式利用二次根式的化简公式及立方根的定义化简,计算即可得到结果;
(2)原式各项化为最简,合并即可得到结果;
(3)原式利用绝对值的代数意义化简,即可得到结果;
(4)方程变形后,利用平方根的定义计算即可求出解.
(2)原式各项化为最简,合并即可得到结果;
(3)原式利用绝对值的代数意义化简,即可得到结果;
(4)方程变形后,利用平方根的定义计算即可求出解.
解答:解:(1)原式=-8×4-4×
-9
=-42;
(2)原式=4
-
+1-
=2
+1;
(3)原式=
-1+
-
+2-
=1;
(4)方程变形得:(x-1)2=
,
开方得:x-1=±
,
解得:x1=
,x2=
.
| 1 |
| 4 |
=-42;
(2)原式=4
| 2 |
| 3 |
| 2 |
| 2 |
| ||
| 2 |
=2
| 2 |
(3)原式=
| 2 |
| 3 |
| 2 |
| 3 |
=1;
(4)方程变形得:(x-1)2=
| 16 |
| 25 |
开方得:x-1=±
| 4 |
| 5 |
解得:x1=
| 9 |
| 5 |
| 1 |
| 5 |
点评:此题考查了实数的运算,涉及的知识有:平方根、立方根的定义,绝对值,以及一元二次方程的解法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
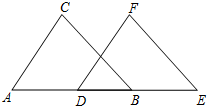 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由. 如图在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的大小为
如图在菱形ABCD中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF的大小为