题目内容
如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点( ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)

①③⑤: 解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣ =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+2=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点( ,0),
,0),
∴抛物线与x轴的另一个交点坐标为( ,0),
,0),
当x=﹣ 时,y=0,即
时,y=0,即 ,
,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴ ,
,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠1),
∴a﹣b>m(am﹣b),所以⑤正确;
故答案为:①③⑤.
点评: 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 的图象位于平面直角坐标系的( )
的图象位于平面直角坐标系的( )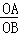 =
=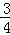 .∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=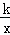 的图象过点C.当以CD为边的正方形的面积为
的图象过点C.当以CD为边的正方形的面积为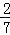 时,k的值是( )
时,k的值是( )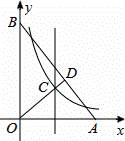

 如图,讲一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相等,则该几何体的左视图是( )
如图,讲一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相等,则该几何体的左视图是( )