题目内容
应用规律,解决问题
(1)定义:a为不等于1的有理数,我们把 称为a的差倒数,如:2的差倒数是
称为a的差倒数,如:2的差倒数是 ,﹣1的差倒数是
,﹣1的差倒数是 ,已知
,已知 ,
,
①a2是a1的差倒数,则a2=_________.
②a3是a2的差倒数,则a3=_________.
③a4是a3的差倒数,则a4=_________.
④以此类推,a2011=_________.
(2)我们知道: ,…,
,…, …×
…× ,试根据上面规律,计算:
,试根据上面规律,计算: …
… .
.
(1)定义:a为不等于1的有理数,我们把
 称为a的差倒数,如:2的差倒数是
称为a的差倒数,如:2的差倒数是 ,﹣1的差倒数是
,﹣1的差倒数是 ,已知
,已知 ,
,①a2是a1的差倒数,则a2=_________.
②a3是a2的差倒数,则a3=_________.
③a4是a3的差倒数,则a4=_________.
④以此类推,a2011=_________.
(2)我们知道:
 ,…,
,…, …×
…× ,试根据上面规律,计算:
,试根据上面规律,计算: …
… .
.解:(1)根据差倒数定义可得:
① =
= =
= ,
,
② =4,
=4,
③ .
.
④显然每三个循环一次,又2011÷3=670余1,故a2011和a1的值相等,∴a2011= ,(2)
,(2) …
… .
.
=﹣ ×(﹣
×(﹣ )×(﹣
)×(﹣ )…(﹣
)…(﹣ ),
),
=﹣ .
.
①
 =
= =
= ,
,②
 =4,
=4,③
 .
.④显然每三个循环一次,又2011÷3=670余1,故a2011和a1的值相等,∴a2011=
 ,(2)
,(2) …
… .
.=﹣
 ×(﹣
×(﹣ )×(﹣
)×(﹣ )…(﹣
)…(﹣ ),
),=﹣
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 【老题重现】
【老题重现】

 ①如图(1),直线l上有2个点,有1条线段;
①如图(1),直线l上有2个点,有1条线段; 称为a的差倒数,如:2的差倒数是
称为a的差倒数,如:2的差倒数是 ,-1的差倒数是
,-1的差倒数是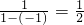 ,已知
,已知 ,
, ,…,
,…, …×
…× ,试根据上面规律,
,试根据上面规律, …
… .
.