题目内容
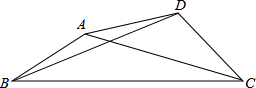 如图,已知△ABC中,∠ABC=30°,AB=2,BC=3
如图,已知△ABC中,∠ABC=30°,AB=2,BC=3| 3 |
考点:相似三角形的判定与性质,含30度角的直角三角形,勾股定理,解直角三角形
专题:
分析:(1)作AE⊥BC于E,求出AE、BE、CE的长度,进而求出AC的长度;
(2)过点D作DG⊥AC于G,由AD=CD,得出AG、CG进,得出AD、DG
(3)作DF⊥AC于F,∠GDH=∠ACE,证明△DGH∽△AEC,求出GH、HC的长度.利用勾股定理求得FC,再得DF.
(4)最后由勾股定理求出BD的长度.
(2)过点D作DG⊥AC于G,由AD=CD,得出AG、CG进,得出AD、DG
(3)作DF⊥AC于F,∠GDH=∠ACE,证明△DGH∽△AEC,求出GH、HC的长度.利用勾股定理求得FC,再得DF.
(4)最后由勾股定理求出BD的长度.
解答: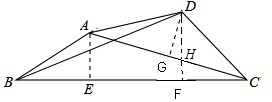 解:作AE⊥BC于E,
解:作AE⊥BC于E,
∵∠ABC=30°,AB=2,
∴AE=1,BE=
.
∴EC=2
,AC=
.
过点D作DG⊥AC于G,
∵AD=CD,DG⊥AC,
∴AG=CG=
.
∵∠ADC=120°,
∴∠DAC=30°
∴AD=
=
=
,DG=
,DC=
.
作DF⊥AC于F,交AC于点H,
∵∠DGC=∠AEC=90°,∠DHG=∠CHF,
∴∠GDH=∠ACE,
又∵∠DGC=∠AEC=90°,
∴△DGH∽△AEC,
∴
=
,GH=
,HC=CG-GH=
.
∵tan∠GDH=
=
又∵∠GDH=∠ACE,
∴
=
,设HF=
x,FC=6x,
在Rt△CHF中,(
x)2+(6x)2=(
)2,
x=
,
FC=
,
在Rt△CDF中,DF=
=
,
BF=BC-FC=3
-
=
,
在Rt△BDF中,BD=
=
=
.
 解:作AE⊥BC于E,
解:作AE⊥BC于E,∵∠ABC=30°,AB=2,
∴AE=1,BE=
| 3 |
∴EC=2
| 3 |
| 13 |
过点D作DG⊥AC于G,
∵AD=CD,DG⊥AC,
∴AG=CG=
| ||
| 2 |
∵∠ADC=120°,
∴∠DAC=30°
∴AD=
| AG |
| cos∠DAC |
| ||||
|
| ||
| 3 |
| ||
| 6 |
| ||
| 3 |
作DF⊥AC于F,交AC于点H,
∵∠DGC=∠AEC=90°,∠DHG=∠CHF,
∴∠GDH=∠ACE,
又∵∠DGC=∠AEC=90°,
∴△DGH∽△AEC,
∴
| DG |
| EC |
| GH |
| AE |
| ||
| 12 |
| 5 |
| 12 |
| 13 |
∵tan∠GDH=
| GH |
| DG |
| ||
| 6 |
又∵∠GDH=∠ACE,
∴
| HF |
| FC |
| ||
| 6 |
| 3 |
在Rt△CHF中,(
| 3 |
| 5 |
| 12 |
| 3 |
x=
| 5 |
| 36 |
| 3 |
FC=
| 5 |
| 6 |
| 3 |
在Rt△CDF中,DF=
| DC2-FC2 |
| 3 |
| 2 |
BF=BC-FC=3
| 3 |
| 5 |
| 6 |
| 3 |
| 13 |
| 6 |
| 3 |
在Rt△BDF中,BD=
| BF2+DF2 |
(
|
| 7 |
| 3 |
| 3 |
点评:本题主要考查了相似三角形的判定与性质以及勾股定理与解直角三角形的综合应用.难度较大,关键是正确地作出辅助线.

练习册系列答案
相关题目
从1,2,3,4,5中随机取出三个不同的数,则其和为奇数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
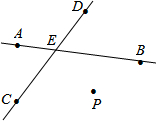 如图,直线CD与直线AB相交于E,根据下列语句画图.
如图,直线CD与直线AB相交于E,根据下列语句画图. 一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是
一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是