题目内容
 如图所示,等腰Rt△ABC内一点D,若AD=2,BD=6,∠ADC=135°,则CD=________.
如图所示,等腰Rt△ABC内一点D,若AD=2,BD=6,∠ADC=135°,则CD=________.
4
分析:如图,把△ACD绕点C旋转90°得△BCD′,根据旋转的性质得△ACD≌△BCD′,可推得A、D、D′三点共线,在直角△DD′B和直角△DCD′中,根据勾股定理,可求得结论;
解答: 解:如图,把△ACD绕点C旋转90°得△BCD′
解:如图,把△ACD绕点C旋转90°得△BCD′
∴△ACD≌△BCD′,
∵△ABC是等腰直角三角形,∠ADC=135°,连接DD′,
∴∠DCD′=90°,∠CD′B=135°,CD=CD′,AD=BD′,
∴△DCD′是等腰直角三角形,即∠DD′B=∠CD′B-∠CD′D=135°-45°=90°,
∴∠CDD′=45°,∴∠ADC+∠CDD′=180°,即A、D、D′三点共线,
∴在直角△DD′B中,BD2=DD′2+BD′2,
又∵在直角△DCD′中,CD2+CD′2=DD′2,
∴2CD2=BD2-BD′2,
即2CD2=36-4=32,
∴CD=4;
故答案为4.
点评:本题考查了等腰直角三角形的性质、全等三角形的判定和性质以及旋转的性质,①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
分析:如图,把△ACD绕点C旋转90°得△BCD′,根据旋转的性质得△ACD≌△BCD′,可推得A、D、D′三点共线,在直角△DD′B和直角△DCD′中,根据勾股定理,可求得结论;
解答:
 解:如图,把△ACD绕点C旋转90°得△BCD′
解:如图,把△ACD绕点C旋转90°得△BCD′∴△ACD≌△BCD′,
∵△ABC是等腰直角三角形,∠ADC=135°,连接DD′,
∴∠DCD′=90°,∠CD′B=135°,CD=CD′,AD=BD′,
∴△DCD′是等腰直角三角形,即∠DD′B=∠CD′B-∠CD′D=135°-45°=90°,
∴∠CDD′=45°,∴∠ADC+∠CDD′=180°,即A、D、D′三点共线,
∴在直角△DD′B中,BD2=DD′2+BD′2,
又∵在直角△DCD′中,CD2+CD′2=DD′2,
∴2CD2=BD2-BD′2,
即2CD2=36-4=32,
∴CD=4;
故答案为4.
点评:本题考查了等腰直角三角形的性质、全等三角形的判定和性质以及旋转的性质,①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
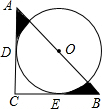 如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )
如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )A、2-
| ||
B、
| ||
C、3-
| ||
| D、2-π |

 如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为
如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为



