题目内容
 如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为
如图所示,等腰RT△ABC分别沿着某条直线对称得到图形b,c,d.若上述对称关系保持不变,平移△ABC,使得四个图形能拼成一个既不重叠且无缝隙的正方形,此时点C的坐标为(
,-
)
| 1 |
| 2 |
| 1 |
| 2 |
(
,-
)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:根据在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等,结合等腰直角三角形的性质,以及正方形的性质可知,△ABC移动时,其它三个对称三角形保持关系不变的随之移动,对称中心也就是最后的四个图形的相交公共点,其在坐标中的位置的横、纵坐标的长度等于右上角的三角形相应边边长的一半,然后根据点在第四象限写出即可.
解答:解:根据图形可知,AC=1,BC=1,
∴移动后,点C的横坐标与纵坐标的长度都是
,
又点C移动后位于第四象限,
∴此时点C的坐标为(
,-
).
故答案为:(
,-
).
∴移动后,点C的横坐标与纵坐标的长度都是
| 1 |
| 2 |
又点C移动后位于第四象限,
∴此时点C的坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了轴对称的性质,以及点的坐标的变化,正方形的性质,利用好有一个三角形的直角顶点正好是坐标原点是解题的关键.

练习册系列答案
相关题目
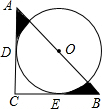 如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )
如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )A、2-
| ||
B、
| ||
C、3-
| ||
| D、2-π |





