题目内容
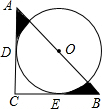 如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )
如图,某工件形状如图所示,等腰Rt△ABC中斜边AB=4,点O是AB的中点,以O为圆心的圆分别与两腰相切于点D、E,则图中阴影部分的面积是( )A、2-
| ||
B、
| ||
C、3-
| ||
| D、2-π |
分析:本题需先求出直角三角形的边长,再利用切线的性质和等腰直角三角形的性质得出四边形CDOE是正方形,然后分别求出直角三角形ABC、扇形FOD,正方形CDOE,扇形EOG的面积,即可求出阴影部分的面积.
解答: 解:设AC=BC=x,
解:设AC=BC=x,
则x2+x2=4
x=2
∴AC=BC=2
设OD=R,则OE=R
∵AC,BC与⊙O相切,
∴OD⊥AD,OE⊥BC
∵∠A=45°
∴∠AOD=45°
∴∠A=∠AOD
∴AD=OD=R
∵AC=2
∵AC=2
∴AD=OD
∵∠C=90°
∴四边形ODCE是正方形
∴CD=CE=OD=AD=
∴S正方形CDOE=(
)2=2
S扇形FOD=S扇形EOG=
=
∴阴影部分的面积是2-
故选A
 解:设AC=BC=x,
解:设AC=BC=x,则x2+x2=4
x=2
| 2 |
∴AC=BC=2
| 2 |
设OD=R,则OE=R
∵AC,BC与⊙O相切,
∴OD⊥AD,OE⊥BC
∵∠A=45°
∴∠AOD=45°
∴∠A=∠AOD
∴AD=OD=R
∵AC=2
| 2 |
∵AC=2
| 2 |
∴AD=OD
∵∠C=90°
∴四边形ODCE是正方形
∴CD=CE=OD=AD=
| 2 |
∴S正方形CDOE=(
| 2 |
S扇形FOD=S扇形EOG=
45π(
| ||
| 360 |
=
| π |
| 4 |
∴阴影部分的面积是2-
| π |
| 2 |
故选A
点评:本题主要考查了扇形面积的求法,在解题时要注意面积计算公式和图形的有关性质的综合应用.

练习册系列答案
相关题目
 某工件形状如图所示,
某工件形状如图所示, |
| BC |
| A、4π | B、6π | C、8π | D、10π |
 的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
 的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
 的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
 的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )
的度数为60°,AB=6cm,点B到点C的距离等于AB,∠BAC=30°,则工件的面积等于( )