题目内容
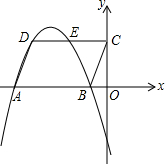 已知:?ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S?ABCD=12,抛物线经过D、A、B三点.
已知:?ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S?ABCD=12,抛物线经过D、A、B三点. (1)求A、C两点的坐标;
(2)求抛物线解析式;
(3)E是抛物线与DC交点,以DE为边的平行四边形,它的面积与?ABCD面积相等,且另两顶点中有一个顶点P在抛物线上,求P点的坐标.
考点:二次函数综合题
专题:
分析:(1)由OB:OC:OA=1:3:5,S?ABCD=12,求得OB=1,OC=3,OA=5,进而求得A、C两点的坐标;
(2)由OB=1,OC=3,OA=5,得出AB=4,根据平行四边形等边平行且相等,得出D(-4,3),然后根据待定系数法即可求得抛物线解析式;
(3)先求得E的坐标,进而求得DE的长,根据以DE为边的平行四边形的面积与?ABCD面积相等,求得P点到直线DE的距离为6,从而求得P的纵坐标为-3,代入抛物线的解析式即可求得P的坐标.
(2)由OB=1,OC=3,OA=5,得出AB=4,根据平行四边形等边平行且相等,得出D(-4,3),然后根据待定系数法即可求得抛物线解析式;
(3)先求得E的坐标,进而求得DE的长,根据以DE为边的平行四边形的面积与?ABCD面积相等,求得P点到直线DE的距离为6,从而求得P的纵坐标为-3,代入抛物线的解析式即可求得P的坐标.
解答:解:(1)∵OB:OC:OA=1:3:5,
设OB=x,OC=3x,OA=5x,
∴AB=OA-OB=5x-x=4x,
∵S?ABCD=12,
∴AB•OC=4x×3x=12,解得x=1,
∴OB=1,OC=3,OA=5,
∴A(-5,0),C(0,3),
(2)∵OB=1,OC=3,OA=5,
∴AB=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴D(-4,3),
∵A(-5,0),B(-1,0),
设抛物线的解析式为y=ax2+bx+c,
∴
,解得
,
∴抛物线的解析式为y=-x2-6x-5.
(3)∵E点的纵坐标为3,
∴-x2-6x-5=3.解得x=-2或x=-4,
∴E的坐标为(-2,3),
∴DE=-2-(-4)=2,
∴以DE为边的平行四边形的面积与?ABCD面积相等,
∴P点到直线DE的距离为,12÷2=6,
∴P的纵坐标为-3,
把y=-3代入y=-x2-6x-5得-x2-6x-5=-3,解得,x=-3+
或x=-3-
,
∴P的坐标为(-3+
,-3)或(-3-
,-3).
设OB=x,OC=3x,OA=5x,
∴AB=OA-OB=5x-x=4x,
∵S?ABCD=12,
∴AB•OC=4x×3x=12,解得x=1,
∴OB=1,OC=3,OA=5,
∴A(-5,0),C(0,3),
(2)∵OB=1,OC=3,OA=5,
∴AB=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴D(-4,3),
∵A(-5,0),B(-1,0),
设抛物线的解析式为y=ax2+bx+c,
∴
|
|
∴抛物线的解析式为y=-x2-6x-5.
(3)∵E点的纵坐标为3,
∴-x2-6x-5=3.解得x=-2或x=-4,
∴E的坐标为(-2,3),
∴DE=-2-(-4)=2,
∴以DE为边的平行四边形的面积与?ABCD面积相等,
∴P点到直线DE的距离为,12÷2=6,
∴P的纵坐标为-3,
把y=-3代入y=-x2-6x-5得-x2-6x-5=-3,解得,x=-3+
| 7 |
| 7 |
∴P的坐标为(-3+
| 7 |
| 7 |
点评:本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
相关题目