Question

如图，等边三角形OAB的边长为2，将线段OB绕着点O逆时针旋转60°得到线段OC，连接BC．
（1）试判定四边形OABC的形状；
（2）求点O到BC的距离；
（3）以O为圆心，r为半径作⊙O，根据⊙O与四边形OABC四条边交点的总个数，求相应r的取值范围．

Answer 1

解：（1）四边形OABC为菱形，
∵△OAB是等边三角形，将线段OB绕着点O逆时针旋转60°得到线段OC，
∴OC=OB，
∴△OCB是等边三角形，
∴四边形OABC为菱形；

（2）如图，过O作OD⊥BC于D，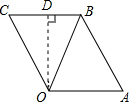
∵△OCB是等边三角形，OB=2，
∴DB=OB，
∴OD=，
即点O到BC的距离为；

（3）当0＜r＜时，⊙O与四边形OABC各边共有2个交点；
当r=时，⊙O与四边形OABC各边共有4个交点；
当＜r＜2时，⊙O与四边形OABC各边共有6个交点；
当r=2时，⊙O与四边形OABC各边共有3个交点；
当r＞2时，⊙O与四边形OABC各边共有0个交点．
分析：（1）四边形OABC为菱形．首先△OAB是等边三角形，然后根据旋转的性质可以得到OC=OB，而旋转角为60°，由此可以得到四边形OABC的形状；
（2）如图，过O作OD⊥BC于D，由于△OCB是等边三角形，由此即可求出OD的长度，也就求出了点O到BC的距离；
（3）根据（2）可以知道O到BC的距离，然后结合图形即可解决问题．
点评：此题分别考查了旋转的性质、菱形的性质及直线与圆的位置关系，同时也利用解直角三角形的知识，综合性比较强，对于学生的要求比较高．