题目内容
 (2013•临沂)如图,等边三角形OAB的一边OA在x轴上,双曲线y=
(2013•临沂)如图,等边三角形OAB的一边OA在x轴上,双曲线y=
| ||
| x |
分析:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),再求出b和a的关系和C点的坐标,由点C在双曲线y=
上,求出a的值,进而求出B点坐标.
| ||
| x |
解答: 解:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),
解:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),
∵三角形OAB是等边三角形,
∴∠BOA=60°,
在Rt△BOA中,tan60°=
=
,
∴b=
a,
∵点C是OB的中点,
∴点C坐标为(
,
),
∵点C在双曲线y=
上,
∴
a2=
,
∴a=2,
∴点B的坐标是(2,2
),
故选C.
 解:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),
解:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),∵三角形OAB是等边三角形,
∴∠BOA=60°,
在Rt△BOA中,tan60°=
| DB |
| OD |
| b |
| a |
∴b=
| 3 |
∵点C是OB的中点,
∴点C坐标为(
| a |
| 2 |
| ||
| 2 |
∵点C在双曲线y=
| ||
| x |
∴
| ||
| 4 |
| 3 |
∴a=2,
∴点B的坐标是(2,2
| 3 |
故选C.
点评:本题主要考查反比例函数的综合题,解答本题的关键是求出点B的坐标,此题难度不大.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
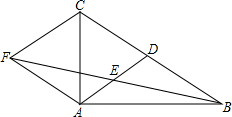 (2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.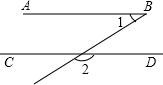 (2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
(2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
 (2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )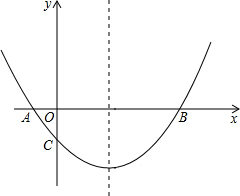 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,