题目内容
如图，⊙O是四边形ABCD的内切圆，下列结论一定正确的是（ ）分析：根据切线长定理得到AF=AE，BF=BG，CG=CH，DH=DE，则AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC．
解答：解：∵⊙O是四边形ABCD的内切圆，
∴AF=AE，BF=BG，CG=CH，DH=DE，
∴AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC．
故选B、C．
∴AF=AE，BF=BG，CG=CH，DH=DE，
∴AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=AD+BC．
故选B、C．
点评：本题考查了切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角．
练习册系列答案
名校课堂系列答案
相关题目
10、如图，l是四边形ABCD的对称轴，如果AD∥BC，有下列结论：①AB∥CD；②AB=BC；③AB⊥BC；④AO=OC，其中正确的结论是
10、如图，L是四边形ABCD的对称轴，如果AD∥BC，则有以下结论：
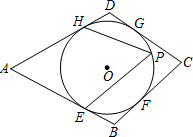（2012•乐山）如图，⊙O是四边形ABCD的内切圆，E、F、G、H是切点，点P是优弧
（保留作图痕迹，写出作法）