题目内容
 如图,AB是⊙O的直径,AC是弦,点D是弧BC的中点,PD切⊙O于点D
如图,AB是⊙O的直径,AC是弦,点D是弧BC的中点,PD切⊙O于点D(1)求证:DP⊥AP;
(2)若PD=
| 3 |
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接BC、OD,则可判断OD∥AP,再由切线的性质可得∠OPD=90°,继而得出结论;
(2)连接OC、CD,由题意可得∠PDC=30°,
(2)连接OC、CD,由题意可得∠PDC=30°,
解答:解:(1)连接BC、OD,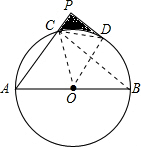 则∠ACB=90°(圆周角定理),
则∠ACB=90°(圆周角定理),
∵点D是弧BC的中点,
∴OD⊥BC,
∴OD∥AP,
又∵PD是⊙O切线,
∴∠OPD=90°,
∴∠P=90°,
∴DP⊥AP.
(2)连接OC、CD,
∵PD=
,PC=1,
∴∠PDC=
=
,CD=
=2,
∴∠PDC=30°,
∴∠CDO=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠COD=∠DOB=∠AOC=60°,
∴△AOC是等边三角形,
∴AO=OC=AC=OD=CD=2,
则S阴影=S梯形ODPA-S△OCA-S扇形OCD=
×(OD+AP)×PD-
-
=
-
-
π=
-
π.
 则∠ACB=90°(圆周角定理),
则∠ACB=90°(圆周角定理),∵点D是弧BC的中点,
∴OD⊥BC,
∴OD∥AP,
又∵PD是⊙O切线,
∴∠OPD=90°,
∴∠P=90°,
∴DP⊥AP.
(2)连接OC、CD,
∵PD=
| 3 |
∴∠PDC=
| PC |
| PD |
| ||
| 3 |
| PC2+PD2 |
∴∠PDC=30°,
∴∠CDO=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠COD=∠DOB=∠AOC=60°,
∴△AOC是等边三角形,
∴AO=OC=AC=OD=CD=2,
则S阴影=S梯形ODPA-S△OCA-S扇形OCD=
| 1 |
| 2 |
| 3 |
| 60π×22 |
| 360 |
5
| ||
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
| 2 |
| 3 |
点评:本题考查了切线的性质、垂径定理、扇形的面积计算及等边三角形的面积,综合考察的知识点较多,注意培养自己解答综合题的能力,将所学知识融会贯通.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
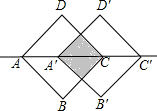 如图,把对角线长为2
如图,把对角线长为2| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
若x=5是分式方程
=
的根,则m的值为( )
| 2 |
| x+3 |
| m |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
 如图,△ABC中,DE∥BC,AD:AB=1:3,则S△ADE:S△ABC=( )
如图,△ABC中,DE∥BC,AD:AB=1:3,则S△ADE:S△ABC=( )| A、1:3 | B、1:5 |
| C、1:6 | D、1:9 |
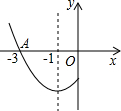 如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=-1,它与x轴的一个交点为A(-3,0),根据图象,可知一元二次方程ax2+bx+c=0的另一个解是
如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=-1,它与x轴的一个交点为A(-3,0),根据图象,可知一元二次方程ax2+bx+c=0的另一个解是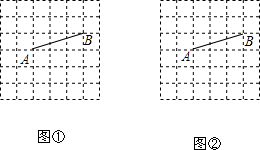 在6×6的正方形网格中,线段AB的端点均在格点上,按下面的要求画图:
在6×6的正方形网格中,线段AB的端点均在格点上,按下面的要求画图: