��Ŀ����
��֪ij������A�ֽ���70�֣�B�ֽ���52�֣��ּƻ��������ֽ�������M��N�����ͺŵĺϽ��Ʒ��80000�ף���֪��һ��M�ͺŵĺϽ��Ʒ��ҪA�ֽ���0.6kg��B�ֽ���0.9kg���ɻ�����45Ԫ����һ��N�ͺŵĺϽ��Ʒ��ҪA�ֽ���1.1kg��B�ֽ���0.4kg���ɻ�����50Ԫ����������N���ͺŵĺϽ��Ʒ����Ϊx�����������������������ͺŵĺϽ��Ʒ����������ΪyԪ��
��1����y��x�ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�������������Ͻ��Ʒʱ��N�ͺŵĺϽ��ƷӦ���������ף��ó��������������������Ƕ��٣�


�⣺��1��y=50x+45��8000��x��=5x+360000��
������ã� ��
��
�ⲻ��ʽ�ٵã�x��44000��
�ⲻ��ʽ�ڵã�x��40000��
���ԣ�����ʽ��Ľ⼯��40000��x��44000��
��y��x�ĺ�����ϵʽ��y=5x+360000��40000��x��44000����
��2����k=5��0��
��y��x�����������
�൱x=44000ʱ��y���=580000��

 ������N�ͺŵ�ʱװ44000��ʱ���ó���������������������580000Ԫ��
������N�ͺŵ�ʱװ44000��ʱ���ó���������������������580000Ԫ��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�ijУ���С�������д��������ÿλѧ����д����39�������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ����.
| ��� | ��д��ȷ�� ����x | ����ֵ |
| A | 0��x<8 | 4 |
| B | 8��x<16 | 12 |
| C | 16��x<24 | 20 |
| D | 24��x<32 | 28 |
| E | 32��x<40 | 36 |

����������Ϣ����������⣺
�� ���ι���������__________��ѧ��������ȫ����ͳ��ͼ��
�� ����ÿ����д��ȷ�ĸ������������ݵ�����ֵ���棬���ѧ����д��ȷ�ĸ�����ƽ�����Ƕ��٣�
�� ��У����3000��ѧ���������д��ȷ�ĸ�������24����Ϊ���ϸ������������ѧУ���α�����д���ϸ��ѧ������.


��ͼ���Ѿ���ֽƬABCD�ضԽ���BD�۵������ص�����Ϊ��EBD��������˵��������ǣ�������

| �� | A�� | AB=CD | B�� | ��BAE=��DCE | C�� | EB=ED | D�� | ��ABEһ������30�� |


 ��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������
��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������

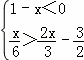 ���������Ľ⼯�������ϱ�ʾ������
���������Ľ⼯�������ϱ�ʾ������ ��ʵ����Χ�������壬��ʵ��
��ʵ����Χ�������壬��ʵ�� ��ȡֵ��Χ�� ( )
��ȡֵ��Χ�� ( ) ��B��
��B�� ��D��
��D��

 ABCD �У���E��AD���е㣬�ӳ�BC����F��ʹCF : BC=1 : 2������DF��EC.��AB=5��AD=8��sinB=
ABCD �У���E��AD���е㣬�ӳ�BC����F��ʹCF : BC=1 : 2������DF��EC.��AB=5��AD=8��sinB= ����DF�ij����� ( )
����DF�ij����� ( ) ��B��
��B�� ��C��
��C�� ��D��
��D��







