题目内容
【题目】如图,抛物线![]() 的图象经过点
的图象经过点![]() ,
,![]() ,
,![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴,且
轴的正半轴,且![]() .
.
(1)求抛物线的函数解析式;
(2)若直线![]() 从点
从点![]() 开始沿
开始沿![]() 轴向下平移,分别交
轴向下平移,分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() .
.
①当![]() 时,在线段
时,在线段![]() 上否存在点
上否存在点![]() ,使得点
,使得点![]() ,
,![]() ,
,![]() 构成等腰直角三角形?若存在,求出点
构成等腰直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
②以动直线![]() 为对称轴,线段
为对称轴,线段![]() 关于直线
关于直线![]() 的对称线段
的对称线段![]() 与二次函数图象有交点,请直接写出
与二次函数图象有交点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;
(2)①点P的坐标是(![]() ,
,![]() )或(3
)或(3![]() 6,3
6,3![]() )或(
)或(![]() ,
,![]() ); ②
); ②![]() .
.
【解析】
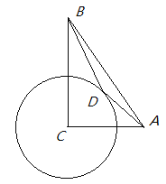
(1)如图1,连结AC.在Rt△AOC中,∠CAB=30°,根据三角函数可得C(0,![]() ),根据待定系数法可求抛物线解析式;
),根据待定系数法可求抛物线解析式;
(2)①由题意可知,OE=m,OD![]() ,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:
,∠DEO=30°,根据等腰直角三角形的判定与性质分三种情况:
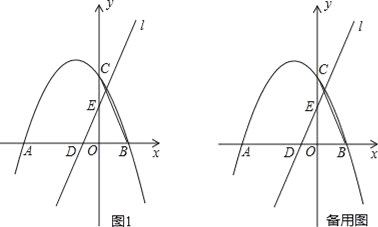
(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴;
(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴;
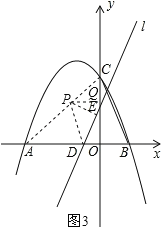
(iii)如图4,当DP⊥DE,DP=PE,作DM⊥AC,EN⊥AC;进行讨论可求点P的坐标;
②动直线l与直线AC的交点为C和动直线l与y轴的交点在x轴下面,并且与前面的直线平行,可求m的取值范围.
(1)如图1,连结AC.在Rt△AOC中,∠CAB=30°.
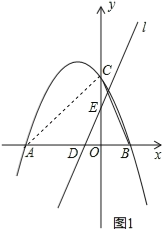
∵A(﹣3,0),即OA=3,
∴OC![]() ,即C(0,
,即C(0,![]() ),
),
设抛物线解析式为![]() ,
,
将A(﹣3,0),B(1,0)代入得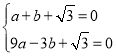 .
.
解得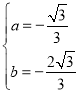 ,
,
∴![]() ;
;
(2)①由题意可知,OE=m,OD![]() ,∠DEO=30°,
,∠DEO=30°,
由A(﹣3,0),C(0,![]() )得到直线AC的解析式为:y
)得到直线AC的解析式为:y![]() x
x![]()
(i)如图2,当PD⊥DE,DP=DE,作PQ⊥x轴,
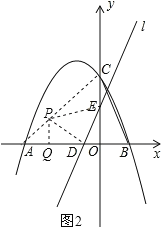
∴∠PQD=∠EOD=90°,∠PDQ+∠EDO=90°,∠EDO+∠DEO=90°,∴∠DEO=∠PDQ=30°,
在△DPQ与△EDO中,
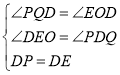 ,
,
∴△DPQ≌△EDO(AAS),
∴DQ=OE=m.
∵∠PAQ=∠PDQ=30°,
∴PA=PD,
∴AQ=DQ=m,
∴OA=2m![]() 3,
3,
∴![]() ;
;
此时P(![]() ,
,![]() )
)
(ii)如图3,当PE⊥DE,PE=DE,作PQ⊥y轴,
同理可得CQ=EQ=OD![]() ,
,
∵OC=m![]() ,
,
∴![]() ;
;
此时P(3![]() 6,3
6,3![]() )
)
(iii)如图4,当DP⊥PE,DP=PE,作DM⊥AC,EN⊥AC,
同理可得AP=AD![]() ,PN=DM
,PN=DM![]() ,CN
,CN![]() ,
,
∴AC![]() ,
,
∴![]() ;
;
此时P(![]() ,
,![]() ).
).
综上所述:点P的坐标是(![]() ,
,![]() )或(3
)或(3![]() 6,3
6,3![]() )或
)或
(![]() ,
,![]() ).
).
②当x=0,y![]() 时,
时,![]() 0+m,解得:m
0+m,解得:m![]() ;
;
当x=0,y![]() 时,
时,![]() 0+m,解得:m
0+m,解得:m![]() .
.
故m的取值范围为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
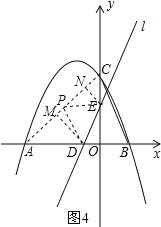
小学生10分钟应用题系列答案【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.4 | 4.3 | ||
卡路里消耗(千卡) | 157 | 79 | 91 | 127 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
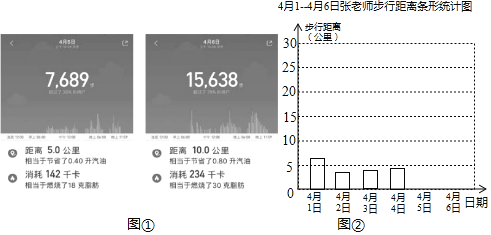
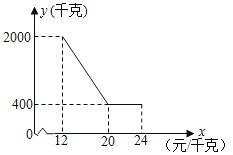
(1)请你将手环记录的4月5日和4月6日的数据(如图①)填入表格
(2)请你将条形统计图(如图②)补充完整
(3)张老师这6天平均每天步行约______公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为______公里(精确到0.1公里)
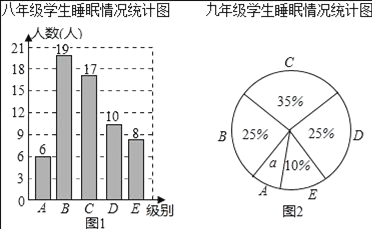
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
|
|
|
|
|
|
|
|
|
|
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中![]() 的值 ;
的值 ;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?