题目内容

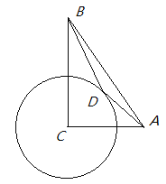
【题目】如图，已知AC=6，BC=8，AB=10，以点C为圆心，4为半径作圆．点D是⊙C上的一个动点，连接AD、BD，则AD+BD的最小值为__________．

【答案】

【解析】

如图，在CB上取一点F，使得CF=2，连接FD，AF.由△FCD∽△DCB，推出，推出DF= BD，推出BD+AD=DF+AD，，根据DF+ADAF即可解决问题.

解：∵AC=6，BC=8，AB=10，

∴,

∴△ABC为Rt△,

在CB上取一点F，使得CF=2，连接FD，AF,如图，


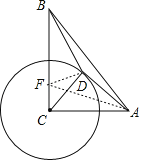
∴CD=4，CF=2，CB=8，
∴，
∵∠FCD=∠DCB，
∴△FCD∽△DCB，
∴，
∴DF= BD，
∴BD+AD=DF+AD，
∵DF+ADAF，AF= = ，
∴BD+AD的最小值是，
故答案为．

练习册系列答案
相关题目

【题目】如图，四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3．分别以点A，C为圆心，大于AC长为半径作弧，两弧交于点E，射线BE交AD于点F，交AC于点O．若点O恰好是AC的中点，则CD的长为__．

【题目】已知坐标平面内抛物线和一点过点作直线，若直线与该抛物线有且只有一个交点，则这样的直线的条数为（ ）

A.0B.1C.2D.3

【题目】已知抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），且满足4a+2b+c＞0，有下列结论：①a+b＞0；②﹣a+b+c＞0；③b2﹣2ac＞5a2．其中，正确结论的个数是（　　）

A. 0B. 1C. 2D. 3

【题目】在平面直角坐标系xOy中抛物线y＝﹣x2+bx+c经过点A、B、C，已知A（﹣1，0），C（0，3）．

（1）求抛物线的表达式；

（2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BCD的面积最大时，求点P的坐标；

（3）如图2，抛物线顶点为E，EF⊥x轴于F点，N是线段EF上一动点，M（m，0）是x轴上一动点，若∠MNC＝90°，直接写出实数m的取值范围．

【题目】如图1，抛物线y＝ax2+bx+c（a≠0）的顶点为C(1，4)，交x轴于A、B两点，交y轴于点D，其中点B的坐标为(3，0)．

（1）求抛物线的解析式；

（2）如图2，点P为直线BD上方抛物线上一点，若，请求出点P的坐标．

（3）如图3，M为线段AB上的一点，过点M作MN∥BD，交线段AD于点N，连接MD，若△DNM∽△BMD，请求出点M的坐标．

【题目】如图①所示，已知正方形ABCD和正方形AEFG，连接DG，BE．

（1）发现：当正方形AEFG绕点A旋转，如图②所示．

①线段DG与BE之间的数量关系是　 　；

②直线DG与直线BE之间的位置关系是　 　；

（2）探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG＝2AE时，上述结论是否成立，并说明理由．

（3）应用：在（2）的情况下，连接BG、DE，若AE＝1，AB＝2，求BG2+DE2的值（直接写出结果）．

【题目】2020年新冠病毒在全球蔓延，口罩成为抗击病毒传播的有效物资，某厂需要生产一批口罩，该厂有甲、乙两种型号的生产机器，若用甲机器单独完成这批订单需要消耗原料费76万元，若用乙机器单独完成需要消耗原料费26万元，已知每生产一个口罩，甲机器消耗原料费比乙机器消耗原料费多用0.5元．

（1）求乙机器生产一个口罩需要消耗多少原料费？

（2）为了尽快完成这批订单，该厂决定使用甲、乙机器一起完成这批订单，消耗原料费合计不超过39万元，则乙机器至少生产多少口罩？

【题目】如图，抛物线的图象经过点，，，已知点的坐标为，点坐标为，点在轴的正半轴，且．

（1）求抛物线的函数解析式；

（2）若直线从点开始沿轴向下平移，分别交轴、轴于点、．

①当时，在线段上否存在点，使得点，，构成等腰直角三角形？若存在，求出点的坐标；若不存在，请说明理由．

②以动直线为对称轴，线段关于直线的对称线段与二次函数图象有交点，请直接写出的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网