题目内容
 直线y=-
直线y=-| 4 |
| 3 |
(1)求A,B两点坐标.
(2)若点P在直线y=-
| 4 |
| 3 |
(3)若⊙P与x轴和直线y=-
| 4 |
| 3 |
分析:(1)已知直线解析式,易求A,B点坐标;
(2)由题意知点P在坐标轴上,说的很模糊,所以要分类讨论,再根据圆的性质及相切的条件,又知道圆的半径,从而求出每种情况的P点坐标;
(3)分P有四种情况,根据勾股定理求得P到选、轴的距离即可求得P的横坐标,则P的坐标可以求得.
(2)由题意知点P在坐标轴上,说的很模糊,所以要分类讨论,再根据圆的性质及相切的条件,又知道圆的半径,从而求出每种情况的P点坐标;
(3)分P有四种情况,根据勾股定理求得P到选、轴的距离即可求得P的横坐标,则P的坐标可以求得.
解答:解:(1)当x=0时,y=4,
当y=0时,-
x+4=0,解得x=3.
 故A(3,0),B(0,4);
故A(3,0),B(0,4);
(2)在y=-
x+4中当y=6时,-
x+4=6,解得:x=-
,则P的坐标是:(-
,6);
在y=-
x+4中当y=-6时,-
x+4=-6,解得:x=
,则P的坐标是(
,-6);
(3)当P的位置如①时,
连接P与切点E,F,则PE⊥x轴,PF⊥AB,作PG∥x轴,交AB于点G,作GH⊥x轴于H.则PE=PF=GH=6,
 在直角△AHG和直角△PFG中,
在直角△AHG和直角△PFG中,
=
=
,
∴AH=GF=
,
∴OH=AH-OA=
-3=
,即H的坐标是(-
,0),
PG=
=
=
,
∴OE=OH+EH=OH+PG=
+
=9,则P的坐标是:(-9,6);
 当P的位置如图②所示时,同①可以得到:AH=GF=
当P的位置如图②所示时,同①可以得到:AH=GF=
,PG=
=
=
,
∴OH=AH-OA=
-3=
,
∴OE=PG-OH=
-
=6,
则P的坐标是(6,6);
当P的位置如图③时,同①可得:AH=
,PG=
则OH=OA+AH=3+
=
,
 ∴OE=OH-EH=OH-PG=
∴OE=OH-EH=OH-PG=
-
=0,则P的坐标是(0,-6);
当P如图④所示时,
AH=
,GP=HE=
,
∴OE=OA+AH+HE=3+
+
=15,
则P的坐标是(15,-6).
总之,P的坐标是:(-9,6)或(6,6)或(0,-6)或(15,-6).
当y=0时,-
| 4 |
| 3 |
 故A(3,0),B(0,4);
故A(3,0),B(0,4);(2)在y=-
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
在y=-
| 4 |
| 3 |
| 4 |
| 3 |
| 15 |
| 2 |
| 15 |
| 2 |
(3)当P的位置如①时,
连接P与切点E,F,则PE⊥x轴,PF⊥AB,作PG∥x轴,交AB于点G,作GH⊥x轴于H.则PE=PF=GH=6,
 在直角△AHG和直角△PFG中,
在直角△AHG和直角△PFG中,| GH |
| AH |
| PF |
| FG |
| 4 |
| 3 |
∴AH=GF=
| 9 |
| 2 |
∴OH=AH-OA=
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
PG=
| PF2+FG2 |
62+(
|
| 15 |
| 2 |
∴OE=OH+EH=OH+PG=
| 3 |
| 2 |
| 15 |
| 2 |
 当P的位置如图②所示时,同①可以得到:AH=GF=
当P的位置如图②所示时,同①可以得到:AH=GF=| 9 |
| 2 |
| PF2+FG2 |
62+(
|
| 15 |
| 2 |
∴OH=AH-OA=
| 9 |
| 2 |
| 3 |
| 2 |
∴OE=PG-OH=
| 15 |
| 2 |
| 3 |
| 2 |
则P的坐标是(6,6);
当P的位置如图③时,同①可得:AH=
| 9 |
| 2 |
| 15 |
| 2 |
则OH=OA+AH=3+
| 9 |
| 2 |
| 15 |
| 2 |
 ∴OE=OH-EH=OH-PG=
∴OE=OH-EH=OH-PG=| 15 |
| 2 |
| 15 |
| 2 |
当P如图④所示时,
AH=
| 9 |
| 2 |
| 15 |
| 2 |
∴OE=OA+AH+HE=3+
| 9 |
| 2 |
| 15 |
| 2 |
则P的坐标是(15,-6).
总之,P的坐标是:(-9,6)或(6,6)或(0,-6)或(15,-6).
点评:本题考查了一次函数与圆的切线的性质,勾股定理的综合应用,正确分情况讨论是关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若直线y=
x-4与x轴正方向的夹角为α,则cosα等于( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
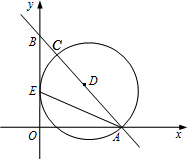 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线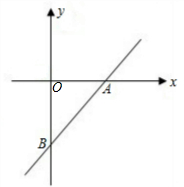 已知:如图,直线
已知:如图,直线