题目内容
直线y=-
x+4和x轴、y轴分别相交于点A、B,在平面直角坐标系内,A、B两点到直线a的距离均为2,则满足条件的直线a的条数为( )
| 4 |
| 3 |
分析:首先画出一次函数图象,再根据A、B两点到直线a的距离均为2可得草图,在直线y=-
x+4的两边各有一条.
| 4 |
| 3 |
解答: 解:∵当x=0时,y=4,
解:∵当x=0时,y=4,
当y=0时,x=3,
∴A(3,0),B(0,4),
如图所示,A、B两点到直线a的距离均为2,这样的直线有2条,
故答案为:B.
 解:∵当x=0时,y=4,
解:∵当x=0时,y=4,当y=0时,x=3,
∴A(3,0),B(0,4),
如图所示,A、B两点到直线a的距离均为2,这样的直线有2条,
故答案为:B.
点评:此题主要考查了一次函数的性质,关键是画出草图,可以直观地得到答案.

练习册系列答案
相关题目
若直线y=
x-4与x轴正方向的夹角为α,则cosα等于( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线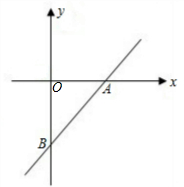 已知:如图,直线
已知:如图,直线