题目内容
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
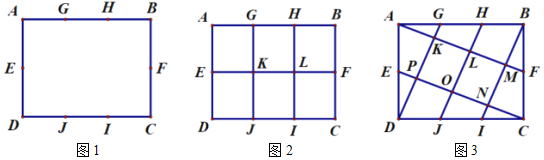
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
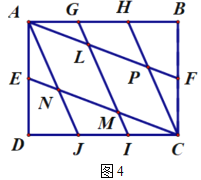
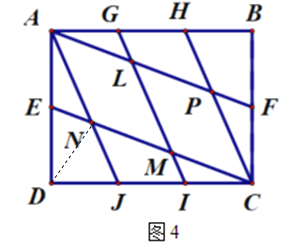
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
【答案】答案见解析.
【解析】试题分析:(1)由六个小长方形的面积相等,得到![]() .设
.设![]() ,
, ![]() .由相似三角形的性质得到:
.由相似三角形的性质得到: ![]() ,
, ![]() .再由
.再由![]() ,
, ![]() ,得到a=
,得到a= ![]() ,
, ![]() =42b,
=42b, ![]() =6b,即可得出结论;
=6b,即可得出结论;
(2)连接DN.设![]() =a,
=a, ![]() =b,则S△EDN=b,S△NJC=4a,S△DNJ=
=b,则S△EDN=b,S△NJC=4a,S△DNJ=![]() S△NJC =2a.由S△ADJ=
S△NJC =2a.由S△ADJ=![]() SABCD,S△CDE=
SABCD,S△CDE=![]() SABCD,得到:b=1.5a,b=
SABCD,得到:b=1.5a,b=![]() SABCD.由S△CFP=S△AEN, SAECF=
SABCD.由S△CFP=S△AEN, SAECF=![]() SABCD, SANML=SMCPL即可得到结论.
SABCD, SANML=SMCPL即可得到结论.
试题解析:解:(1) ∵六个小长方形的面积相等,∴![]() .
.
设![]() ,
, ![]() .∵EC∥AF,∴△DEP∽△DAK,且相似比为1:2,得到
.∵EC∥AF,∴△DEP∽△DAK,且相似比为1:2,得到![]() .∵GD∥BI,∴△AGK∽△ABM,且相似比为1:3,得到
.∵GD∥BI,∴△AGK∽△ABM,且相似比为1:3,得到![]() .又∵
.又∵![]() ,
, ![]() ,∴
,∴![]() ,
,
∴a= ![]() ,
, ![]() =42b,
=42b, ![]() =6b,∴
=6b,∴![]() ,则
,则![]() ;
;
(2)连接DN.设![]() =a,
=a, ![]() =b,则S△EDN=b,S△NJC=4a,S△DNJ=
=b,则S△EDN=b,S△NJC=4a,S△DNJ=![]() S△NJC =2a.∵S△ADJ=
S△NJC =2a.∵S△ADJ=![]() SABCD,S△CDE=
SABCD,S△CDE=![]() SABCD,∴2b+2a=
SABCD,∴2b+2a=![]() SABCD,b+6a=
SABCD,b+6a=![]() SABCD, 解得:b=1.5a,b=
SABCD, 解得:b=1.5a,b=![]() SABCD.∵S△CFP=S△AEN, SAECF=
SABCD.∵S△CFP=S△AEN, SAECF=![]() SABCD,∴SANML=SMCPL=(
SABCD,∴SANML=SMCPL=(![]() SABCD-2×
SABCD-2×![]() SABCD)×
SABCD)×![]() =
=![]()
![]() .
.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?