题目内容
【题目】已知圆锥的高为![]() ,母线为
,母线为![]() ,且
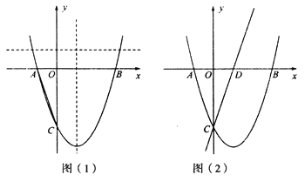
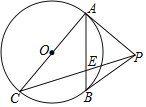
,且![]() ,圆锥的侧面展开图为如图所示的扇形.将扇形沿
,圆锥的侧面展开图为如图所示的扇形.将扇形沿![]() 折叠,使
折叠,使![]() 点恰好落在
点恰好落在![]() 上的
上的![]() 点,则弧长
点,则弧长![]() 与圆锥的底面周长的比值为( )
与圆锥的底面周长的比值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
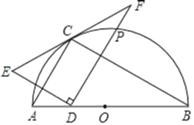
连接AF,如图,设OB=5a,AB=18a,∠BAC=n°,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到![]() ,解得n得到∠BAC=100°,再根据折叠的性质得到BA=BF,则可判断△ABF为等边三角形,于是可计算出∠FAC=40°,然后根据弧长公式计算弧长CF与圆锥的底面周长的比值.
,解得n得到∠BAC=100°,再根据折叠的性质得到BA=BF,则可判断△ABF为等边三角形,于是可计算出∠FAC=40°,然后根据弧长公式计算弧长CF与圆锥的底面周长的比值.
连接AF,如图,
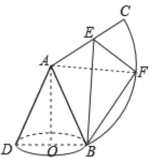
设OB=5a,AB=18a,∠BAC=n°
∴![]() ,
,
解得n=100
即∠BAC=100°
∵将扇形沿BE折叠,使A点恰好落在![]() 上F点,
上F点,
∴BA=BF
而AB=AF
∴△ABF为等边三角形
∴∠BAF=60°
∴∠FAC=40°
∴![]() 的长度=
的长度=![]()
∴弧长CF与圆锥的底面周长的比值=![]()
故选:B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
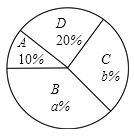
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.