题目内容
17. 如图,方格纸中每个小正方形的边长都是1个单位长度.Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)
如图,方格纸中每个小正方形的边长都是1个单位长度.Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)(1)将△ABC以点O为旋转中心旋转180°,得到△A1B1C1,请画出△A1B1C1的图形.
(2)将△ABC以C为旋转中心,逆时针旋转90°.得到△A2B2C2,请画出△A2B2C2的图形.
(3)线段BB2的长度为5$\sqrt{2}$.
分析 (1)将△ABC以点O为旋转中心旋转180°即可.
(2)将△ABC以C为旋转中心,逆时针旋转90°即可.
(3)在RT△BOB2中利用勾股定理即可.
解答 解:(1)△A1B1C1的图形如图所示.
(2)△A2B2C2的图形如图所示,.
(3) 在RT△BOB2中,BB2=$\sqrt{O{B}^{2}+{B}_{2}{O}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$.
在RT△BOB2中,BB2=$\sqrt{O{B}^{2}+{B}_{2}{O}^{2}}$=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$.
故答案为5$\sqrt{2}$.
点评 本题考查中心旋转的性质、勾股定理等知识,熟练掌握中心旋转的定义是解决问题的关键,作中心旋转图形时注意需要每个点绕旋转中心旋转,旋转角度相同,属于基础题,中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.估计$\sqrt{10}$的值在哪两个整数之间( )
| A. | 9和10 | B. | 7和8 | C. | 5和6 | D. | 3和4 |
 如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?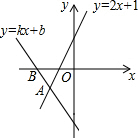 如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.
如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.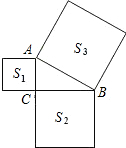 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边向外作正方形,S1、S2、S3分别表示这三个正方形的面积,S1=4,S3=25,则S2=21.