题目内容
解下列方程：
（1）9（x-2）2=4（x+1）2；
（2）（3x-1）2-4（2x+3）2=0．
（1）9（x-2）2=4（x+1）2；
（2）（3x-1）2-4（2x+3）2=0．
考点：解一元二次方程-因式分解法
专题：计算题
分析：（1）方程变形后，利用平方差公式分解，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解；
（2）方程左边利用平方差公式分解，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
（2）方程左边利用平方差公式分解，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
解答：解：（1）方程变形得：9（x-2）2-4（x+1）2=0，
分解因式得：[3（x-2）+2（x+1）][3（x-2）-2（x+1）]=0，
解得：x1=1，x2=8；
（2）分解因式得：[3x-1+2（2x+3）][3x-1-2（2x+3）]=0，
解得：x1=-
，x2=-1．
分解因式得：[3（x-2）+2（x+1）][3（x-2）-2（x+1）]=0，
解得：x1=1，x2=8；
（2）分解因式得：[3x-1+2（2x+3）][3x-1-2（2x+3）]=0，
解得：x1=-
| 5 |
| 7 |
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解法是解本题的关键．
练习册系列答案
相关题目
如图所示是一次函数y=mx+n的图象，当x≥0时，则（ ）| A、y≥0 | B、y≥2 |
| C、y≥1 | D、y≤2 |
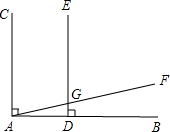如图，已知AC⊥AB，ED⊥AB，∠CAF=78°，求∠DGF的度数．