题目内容
我们知道：
1+3=4=22；
1+3+5=9=32；
1+3+5+7=16=42；
1+3+5+7+9=25=52．
根据前面各式规律，可以猜测：
1+3+5+7+9+…+（2n-1）=________．（其中n为自然数）．
n2
试题分析：从数字中找到规律，从小范围到大范围．
从1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，三个等式中，可以看出等式左边最后一个数+1再除以2即得到等式右边幂的底数，
即1+3+5+7+9+…+（2n-1）=n2．
考点：本题考查的是找规律
点评：解答本题的关键是认真分析所给式子，得出规律，再应用发现的规律解决问题
试题分析：从数字中找到规律，从小范围到大范围．
从1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，三个等式中，可以看出等式左边最后一个数+1再除以2即得到等式右边幂的底数，
即1+3+5+7+9+…+（2n-1）=n2．
考点：本题考查的是找规律
点评：解答本题的关键是认真分析所给式子，得出规律，再应用发现的规律解决问题
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
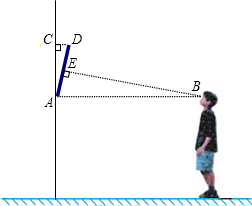知装饰画的高度AD为0.66米，
