题目内容
【题目】在![]() 中,
中,![]() ,
,![]() .
.
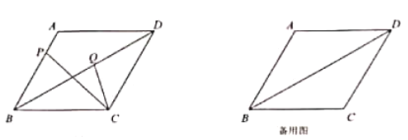
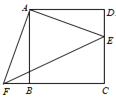
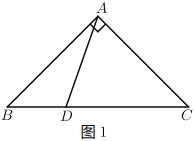
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
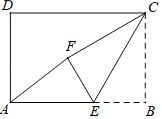
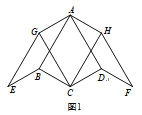
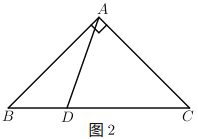
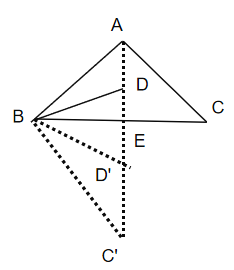
(2)如图2,若![]() 为线段
为线段![]() 上任意一点,探究
上任意一点,探究![]() ,
,![]() ,
,![]() 三者之间的关系,并证明.
三者之间的关系,并证明.
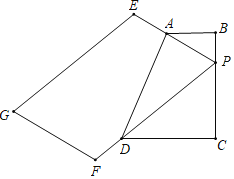
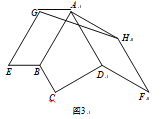
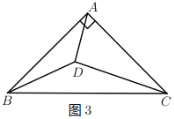
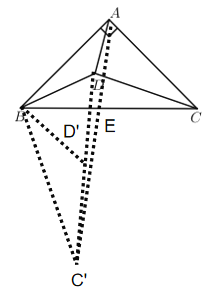
(3)如图3,若![]() ,
,![]() 为
为![]() 内一点,求
内一点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
(1)根据![]() ,可得
,可得![]() ,即可求解.
,即可求解.
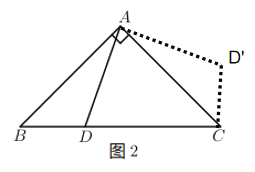
(2)将△ABD绕点A逆时针旋转90°,点B对应点C,点D对应点![]() ,由旋转的性质和勾股定理可得
,由旋转的性质和勾股定理可得![]() ,即
,即![]() ,即可得证
,即可得证![]() .
.
(3)将△BDC绕点B顺时针旋转60°,得到△![]() ,连接
,连接![]() ,连接
,连接![]() 交BC于点E,通过等边三角形的性质和旋转的性质可得当
交BC于点E,通过等边三角形的性质和旋转的性质可得当![]() 时,
时,![]() 有最小值,根据勾股定理求解即可.
有最小值,根据勾股定理求解即可.
(1)∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]() .
.
(2)![]()
将△ABD绕点A逆时针旋转90°,点B对应点C,点D对应点![]()
由旋转的性质得![]()
∴![]()
∴在Rt△![]() 中,
中,![]()
∵在Rt△![]() 中,
中,![]()
∴![]()
∴![]()
即![]() .
.
(3)将△BDC绕点B顺时针旋转60°,得到△![]() ,连接
,连接![]() ,连接
,连接![]() 交BC于点E
交BC于点E
∵![]()
∴![]() 为等边三角形
为等边三角形
∴![]()
∵![]()
∴![]()
∴![]() 的最小值为
的最小值为![]() 的最小值
的最小值
故当![]() 时,
时,![]() 有最小值
有最小值
∵![]()
∴△ABC是等腰直角三角形
∵![]()
∴![]()
即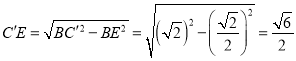 ,
,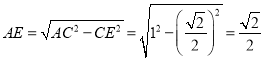
即![]()
∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目