题目内容
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN,则重叠部分(△DMN)的面积为 .

 解:如图所示:
解:如图所示:
过点D作DK⊥AC于点K,则DK∥BC,
又∵点D为AB中点,
∴DK= BC=3.
BC=3.
∵DM=MN,∴∠MND=∠MDN,由∠MDN=∠B,
∴∠MND=∠B,又∵∠DKN=∠C=90°,
∴△DKN∽△ACB,
∴ =
= ,即
,即 =
= ,得KN=
,得KN= .
.
设DM=MN=x,则MK=x﹣ .
.
在Rt△DMK中,由勾股定理得:MK2+DK2=MD2,
即:(x﹣ )2+32=x2,解得x=
)2+32=x2,解得x= ,
,
∴S△DMN= MN•DK=
MN•DK= ×
× ×3=
×3= .
.
故答案为: .
.


练习册系列答案
相关题目



 B.
B. C.
C.
 D.
D. 

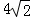 ,求点G到BE的距离.
,求点G到BE的距离.

