题目内容
有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖直放就比门高0.5米，斜放恰好等于门的对角线长．已知门宽1.5米，求门的高度．
考点：勾股定理的应用
专题：
分析：根据题中所给的条件可知，竹竿斜放就恰好等于门的对角线长，可与门的宽和高构成直角三角形，运用勾股定理可求出门高．
解答：解：设门高为xm，则竹竿长为（x+0.5）m，
根据勾股定理可得：
x2+1.52=（x+0.5）2，
解得：x=2．
答：门高2m．
根据勾股定理可得：
x2+1.52=（x+0.5）2，
解得：x=2．
答：门高2m．
点评：本题考查勾股定理的运用，正确运用勾股定理，将数学思想运用到实际问题中是解答本题的关键，难度一般．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
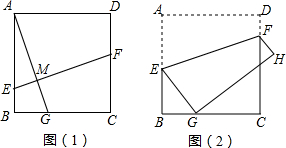
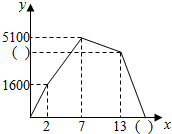甲骑自行车，乙步行均从A地出发，以各自的速度匀速向B地行驶，其中甲先出发到达B地，停留6分钟后，按原路原速返回到A地，乙则一直步行到B地，如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象．
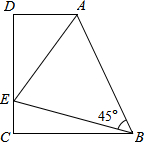如图，在梯形ABCD中，AD∥BC（BC＞AD），∠D=90°，BC=CD=12，∠ABE=45°，若AE=10．求CE的长度．已知圆柱的母线长5，侧面积为30π，则圆柱的底面直径长是（ ）
| A、3 | B、6 | C、9 | D、12 |
如图，二次函数y=ax2+mc（a≠0）的图象经过正方形ABOC的三个顶点，且ac=-2，则m的值为
如图，⊙O直径AB=8，∠CBD=30°，则CD=（ ）| A、4 | ||
| B、6 | ||
| C、3 | ||
D、2
|
二次函数y=x2-4x+3的图象与x轴的交点坐标是（ ）
| A、（1，0），（-3，0） |
| B、（1，0），（3，0） |
| C、（-1，0），（-3，0） |
| D、（3，0），（-1，0） |
比较-2.4，+（-0.5），-（-2），-|-3|的大小，下列正确的是（ ）
| A、-|-3|＞-2.4＞-（-2）＞+（-0.5 ） |
| B、-（-2）＞-|-3|＞-2.4＞+（-0.5） |
| C、-（-2）＞+（-0.5）＞-2.4＞-|-3| |
| D、-|-3|＞-（-2）＞-2.4＞+（-0.5） |