题目内容
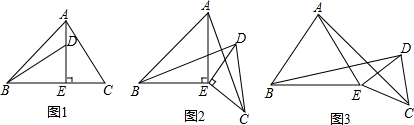
(1)如图1,在正方形ABCD中,点E、F、G分别在AB、CD、BC上,且EF⊥AG,垂足为M,那么AG与EF (“相等”或“不相等”)
(2)如图2,将边长为8cm的正方形纸片ABCD沿EF折叠,使得点A落到边BC上.若BG=2cm,求出BE和EF的长度.
(2)如图2,将边长为8cm的正方形纸片ABCD沿EF折叠,使得点A落到边BC上.若BG=2cm,求出BE和EF的长度.

考点:正方形的性质,全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)可过点E作EH∥AD,证明Rt△ABG≌Rt△EHF即可得出结论.
(2)借助对称原理,根据勾股定理即可求出BE、AG的长;利用第(1)问中的结论即可获得EF的长.
(2)借助对称原理,根据勾股定理即可求出BE、AG的长;利用第(1)问中的结论即可获得EF的长.
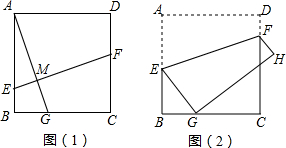
解答:解:(1)如图(1)所示,过点E作EH∥AD,交CD于H;则四边形AEHD为矩形;
∴EH=AD=AB;
∵AG⊥EF,EH∥AD,
∴∠BAG+∠AEF=90°,∠AEF+∠FEH=90°,
∴∠BAG=∠FEH;在△ABG与△EHF中,
∵
,∴△ABG≌△EHF(ASA)
∴AG=EF.
故答案为相等;
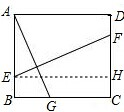
(2)如图(2),连接AG;
设BE=x,则AE=8-x;由对称原理得:EG=EA=8-x,∠AEF=∠GEF,
∴EF⊥AG;由问题(1)知:EF=AG;
∵四边形ABCD为正方形,∴∠EBG=90°;
由勾股定理得:AG2=82+22,AG=2
;
(8-x)2=x2+22,解得x=
,
∴BE=
(cm),EF=2
(cm).

∴EH=AD=AB;
∵AG⊥EF,EH∥AD,
∴∠BAG+∠AEF=90°,∠AEF+∠FEH=90°,
∴∠BAG=∠FEH;在△ABG与△EHF中,
∵
|
∴AG=EF.
故答案为相等;

(2)如图(2),连接AG;
设BE=x,则AE=8-x;由对称原理得:EG=EA=8-x,∠AEF=∠GEF,
∴EF⊥AG;由问题(1)知:EF=AG;
∵四边形ABCD为正方形,∴∠EBG=90°;
由勾股定理得:AG2=82+22,AG=2
| 17 |
(8-x)2=x2+22,解得x=
| 15 |
| 4 |
∴BE=
| 15 |
| 4 |
| 17 |

点评:本题考查了全等三角形的判定及其性质、勾股定理、对称原理及其应用问题;对综合的分析问题、解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
关于x的一元二次方程x2+nx+m=0的两根中只有一个等于0,则下列条件正确的是( )
| A、m=0,n=0 |
| B、m≠0,n≠0 |
| C、m≠0,n=0 |
| D、m=0,n≠0 |
若a表示有理数,则-a是( )
| A、正数 | B、负数 |
| C、a的相反数 | D、a的倒数 |
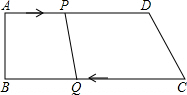 在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=25cm,BC=26cm;点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时另一个动点也停止运动,从运动开始.使PQ=CD,需经过多少时间?
在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=25cm,BC=26cm;点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时另一个动点也停止运动,从运动开始.使PQ=CD,需经过多少时间?