题目内容
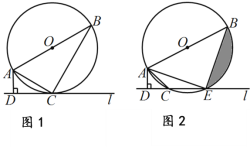
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
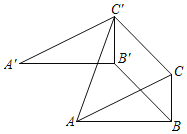
(3)若点![]() 是点
是点![]() 关于直线OE的对称点,是否存在点
关于直线OE的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 上?若存在,请直接写出相应的点
上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,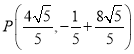
【解析】
(1)利用待定系数法求出抛物线的解析式;
(2)用含m的代数式分别表示出PE、EF,然后列方程求解;
(3)根据题意作出示意图,根据点![]() 、
、![]() 关于直线OE对称,得到
关于直线OE对称,得到![]() ,由平行得到
,由平行得到![]() ,故
,故![]() ,于是
,于是![]() ,设
,设![]() ,求出
,求出![]() ,得到
,得到![]() ,解出m的值即可求解.
,解出m的值即可求解.
解:(1)将点![]() 、
、![]() 坐标代入抛物线解析式,得:
坐标代入抛物线解析式,得:
![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:![]() .
.
(2)∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
由题意,![]() ,即:
,即:![]()
①若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() ;
;
②若![]() ,整理得:
,整理得:![]() ,
,
解得:![]() 或
或![]() .
.
由题意,![]() 的取值范围为:
的取值范围为:![]() ,
,
∴![]() 或
或![]() .
.
(3)假设存在.
作出示意图如下:
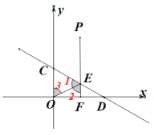
∵点![]() 、
、![]() 关于直线OE对称,
关于直线OE对称,
∴![]() ,
,
∵![]() 平行于
平行于![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
设![]()
∴![]() ,
,
∴![]() .
.
解得![]() 或
或![]() (负值舍去)
(负值舍去)
把x=![]() 代入抛物线得到
代入抛物线得到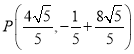 .
.
故存在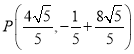 使点
使点![]() 落在
落在![]() 上.
上.

【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
【题目】小魏探究学习函数的经验,对函数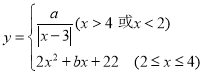 的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
的图像与性质进行了研究,下面是小魏的探究过程,请补充完整.
(1)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请直接写出:![]() _______,
_______,![]() ______,
______,![]() _______.
_______.
(2)画出该函数图像.
(3)写出该函数的一条性质:_______________.
(4)一次函数![]() 与该函数图像至少有三个交点,则
与该函数图像至少有三个交点,则![]() 的范围_______.
的范围_______.
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.