题目内容

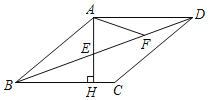
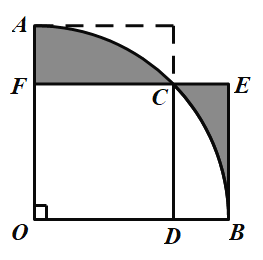
【题目】如图，扇形AOB的圆心角为直角，边长为1的正方形ODCF的顶点F，D，C分别在OA，OB，上，过点B作BE⊥FC，交FC的延长线于点E，则图中阴影部分的面积等于__．

【答案】

【解析】

如下图，过点A作DC的垂线，交DC延长线于点G，先推导出阴影部分CEB的面积等于ACG围成图形的面积，从而将图形中阴影部分面积转化为矩形AFCG的面积求解．

如下图，过点A作DC的垂线，交DC延长线于点G，连接OC

∵四边形ODCF是正方形，边长为1

∴∠AOC=∠COB=45°，OC=

∴点C是AB的中点，OA=OB=OC=

由图形可得：阴影部分CEB的面积等于ACG围成图形的面积

∴图形阴影部分面积可转化为矩形AFCG的面积

AF=OA-OF=，FC=1

∴矩形AFCG的面积为：()×1=

故答案为：．

练习册系列答案
相关题目

【题目】如图，矩形ABCD中，AB=8cm，BC=6cm，点P从点A出发，以lcm/s的速度沿A→D→C方向匀速运动，同时点Q从点A出发，以2cm/s的速度沿A→B→C方向匀速运动，当一个点到达点C时，另一个点也随之停止．设运动时间为t（s），△APQ的面积为S（cm2），下列能大致反映S与t之间函数关系的图象是（　　）

A. B. C. D.

【题目】已知y关于x的二次函数y=x-bx+b+b-5的图象与x轴有两个公共点．

（1）求b的取值范围；

（2）若b取满足条件的最大整数值，当m≤x≤时，函数y的取值范围是n≤y≤6-2m，求m，n的值；

（3）若在自变量x的值满足b≤x≤b+3的情况下，对应函数y的最小值为，求此时二次函数的解析式．

【题目】如图1，抛物线与轴交于、，交轴于点．

（1）抛物线顶点的坐标为________；

（2）如图2，连接、．将沿轴方向以每秒1个单位长度的速度向右平移得到，运动时间为秒．当时，求与重叠面积与的函数解析式，并求出的最大值；

（3）如图3中，将绕点顺时针旋转一定的角度得到，边与抛物线的对称轴交于点．在旋转过程中，是否存在一点，使得？若存在，直接写出所有满足条件的点的坐标；若不存在，请说明理由．

【题目】如图，抛物线与轴交于点，两点，直线与轴交于点，与轴交于点．点是轴上方的抛物线上一动点，过点作轴于点，交直线于点．设点的横坐标为．

（1）求抛物线的解析式；

（2）若，求的值；

（3）若点是点关于直线OE的对称点，是否存在点，使点落在上？若存在，请直接写出相应的点的坐标；若不存在，请说明理由．

【题目】如图1，平行四边形ABCD中，AB⊥AC，AB＝3，AD＝5，点P在边AD上运动，以P为圆心，PA为半径的⊙P与对角线AC交于A，E两点．

（1）如图2，当⊙P与边CD相切于点F时，求AP的长；

（2）不难发现，当⊙P与边CD相切时，⊙P与平行四边形ABCD的边有三个公共点，随着AP的变化，⊙P与平行四边形ABCD的边的公共点的个数也在变化，若公共点的个数为4，直接写出相对应的AP的值的取值范围．

【题目】如图，BM是以AB为直径的⊙O的切线，B为切点，BC平分∠ABM，弦CD交AB于点E，DE＝OE．

（1）求证：△ACB是等腰直角三角形；

（2）求证：OA2＝OEDC：

（3）求tan∠ACD的值．

【题目】如图，在菱形ABCD中，过点A作AH⊥BC，分别交BD，BC于点E，H，F为ED的中点，∠BAF＝120°，则∠C的度数为_____．

【题目】如图，在ABCD中，∠C＝30°，过D作DE⊥BC于点E，延长CB至点F，使BF＝CE，连接AF．若AF＝4，CF＝10，则ABCD的面积为_____．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网