题目内容
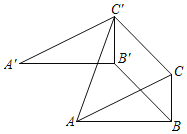
【题目】定义:有一组邻边相等的凸四边形叫做等邻边四边形.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB'的方向平移,得到A'B'C',连接AC',CC',若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是_____.
【答案】1或![]() .
.
【解析】
由平移的性质得到![]() ,① 当
,① 当![]() 时,
时,![]() ;② 如图1,当
;② 如图1,当![]() 时,③如图2,当
时,③如图2,当![]() 时,则
时,则![]() ,延长
,延长![]() 交AB于H,设
交AB于H,设![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
解:∵将Rt△ABC平移得到![]() ,
,
![]() ,
,
① 当![]() 时,
时,![]() ;
;
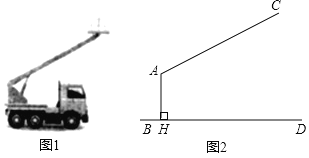
②如图1,当![]() 时,
时,
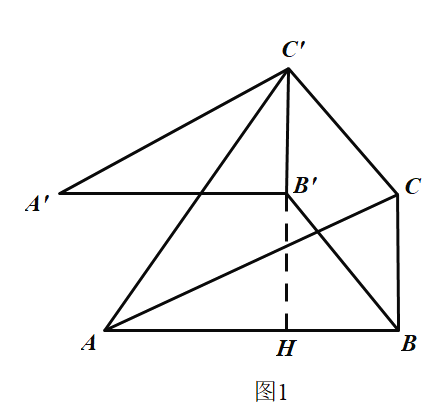
∵∠ABC=90°,![]() 是∠ABC的角平分线,
是∠ABC的角平分线,
∴![]() ,
,
延长![]() 交AB于H,
交AB于H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
![]()
∴22=(2﹣x)2+(1+x)2,
整理方程为:2x2﹣2x+1=0,
∵△=4﹣8=﹣4<0,
∴此方程无实数根,故这种情况不存在;
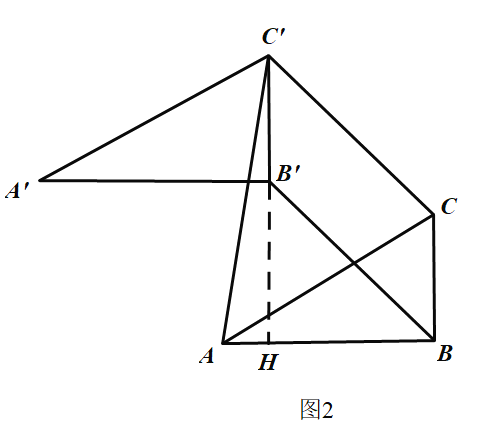
③如图2,当当![]() 时,则
时,则![]() ,
,
延长![]() 交AB于H,
交AB于H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
![]()
∴(![]() x)2=(2﹣x)2+(1+x)2,
x)2=(2﹣x)2+(1+x)2,
解得:x=![]() ,
,
∴BB′=![]() ,
,
综上所述,若四边形ABCC'是等邻边四边形,则平移距离BB'的长度是1或![]() ,
,
故答案为:1或![]() .
.

练习册系列答案
相关题目